摘要:如图.在直角坐标系中.点A.B.C的坐标分别为.过A.B.C三点的抛物线的对称轴为直线.D为对称轴上一动点. ① 求抛物线的解析式, ② 求当AD+CD最小时点D的坐标.并求出AD+CD的最小值.
网址:http://m.1010jiajiao.com/timu3_id_492071[举报]
(本题12分) 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=![]() ,直线y=经过点C,交y轴于点G,且∠AGO=30°。
,直线y=经过点C,交y轴于点G,且∠AGO=30°。
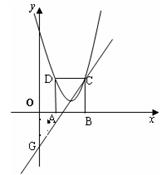
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y=![]() 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
查看习题详情和答案>>
(本题12分)如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
(1)当∠AOB=30°时,求弧AB的长度;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
查看习题详情和答案>>
(本题12分)如图,在平面直角坐标系中,等腰梯形OABC,CB//OA,且点A在x轴正半轴上.已知C(2,4),BC=4.
(1)求过O、C、B三点的抛物线解析式,并写出顶点坐标和对称轴;
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合),使得P点到两坐标轴的
距离相等.如果存在,求出P点坐标;如果不存在,请说明理由.
查看习题详情和答案>>
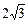 ,直线y=
,直线y=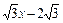 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。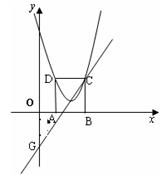
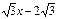 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。