摘要：已知y=y1-y2,其中y1是x的反比例函数,y2是x2的正比例函数,且x=1时y=3,x=-2时y=-15. 求:(1)y与x之间的函数关系式; (2)当x=2时y的值. (1)答案:y=-3x2. 提示:y1是x的反比例函数.可设y1=.y2是x2的正比例函数.可设y2=k2x2.则y与x的关系式为y=-k2x2.x=1时y=3;x=-2时y=-15.代入求出k1=6.k2=3. (2)答案:-9. 提示:将x=2代入解析式y=-3x2.y=3-3×4=-9.
网址：http://m.1010jiajiao.com/timu3_id_490094[举报]
反比例函数y1=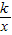
图象上的一些点的坐标如下表所示：
（1）这个反比例函数的表达式是______；
（2）一次函数的表达式是y2=mx-1（其中，m是常数，且m≠0）．
①求证：不论m为何值，该一次函数的图象都经过一个定点；
②已知一次函数的图象与反比例函数图象交于点（-6，1）和点（3，-2），请你直接写出使式子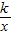
＞mx-1成立的x的取值范围．
查看习题详情和答案>>
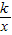图象上的一些点的坐标如下表所示：| x | … | -3 | -2 | -1 | … | 1 | 2 | 3 | … |
| y | … | 2 | 3 | 6 | … | -6 | -3 | -2 | … |
（2）一次函数的表达式是y2=mx-1（其中，m是常数，且m≠0）．
①求证：不论m为何值，该一次函数的图象都经过一个定点；
②已知一次函数的图象与反比例函数图象交于点（-6，1）和点（3，-2），请你直接写出使式子
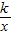＞mx-1成立的x的取值范围．查看习题详情和答案>>
反比例函数y1=
图象上的一些点的坐标如下表所示：
| x | … | -3 | -2 | -1 | … | 1 | 2 | 3 | … |
| y | … | 2 | 3 | 6 | … | -6 | -3 | -2 | … |
（2）一次函数的表达式是y2=mx-1（其中，m是常数，且m≠0）．
①求证：不论m为何值，该一次函数的图象都经过一个定点；
②已知一次函数的图象与反比例函数图象交于点（-6，1）和点（3，-2），请你直接写出使式子
＞mx-1成立的x的取值范围．
查看习题详情和答案>>
反比例函数y1＝
图象上的一些点的坐标如下表所示：
| x | … | －3 | －2 | －1 | … | 1 | 2 | 3 | … |
| y | … | 2 | 3 | 6 | … | －6 | －3 | －2 | … |
(1)这个反比例函数的表达式是 ；
(2)一次函数的表达式是y2＝mx－1(其中，m是常数，且m≠0)．
①求证：不论m为何值，该一次函数的图象都经过一个定点；
②已知一次函数的图象与反比例函数图象交于点(－6，1)和点(3，－2)，请你直接写出使式子
＞mx－1成立的x的取值范围．
已知正比例函数y1=x，反比例函数