摘要：如图.AB是⊙O是直径.过A作⊙O的切线.在切线上截取AC=AB.连结OC交⊙O于D.连结BD并延长交AC于E.⊙F是△ADE的外接圆.⊙F在AE上. 求证:(1)CD是⊙F的切线, (2)CD=AE. 证明:(1)连接DF ∵CA 切⊙O于A.∴∠CAB=90° 又∵∠OAD=∠ODA ∠FAD=∠FDA ∴∠OAC=∠ODF=90° ∴∠FDC=90 ∴CD是⊙F的切线 (2)FDC=DAC=90 ∠C=∠C ∴△CDF∽△CAO 又∵AC=AB ∴== 又∵DF=FE AE=2DF ∴AE=CD
网址：http://m.1010jiajiao.com/timu3_id_489036[举报]
如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆弧上．①若正方形的顶点F也在半圆弧上，则半圆的半径与正方形边长的比是| 5 |
| 5 |
100
100
．
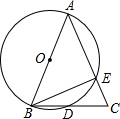如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°．给出以下五个结论：①∠EBC=22.5°；②AE=BC；③AE=2EC；④劣弧AE是劣弧DE的2倍；⑤BD=DC．其中正确结论的序号是①④⑤
①④⑤
．
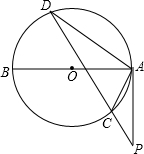（2012•泰宁县质检）已知，如图，AB为⊙O的直径，弦DC延长线上有一点P，∠PAC=∠PDA．（1）求证：PA是⊙O的切线；
（2）若AD=6，∠ACD=60°，求⊙O的半径．
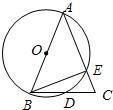已知：如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45度．给出以下五个结论：①∠EBC=22.5°；②BD=DC；③AE=2EC；④劣弧AE是劣弧DE的2倍；⑤AE=BC．其中正确结论的序号是（ ）
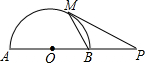如图，AB为⊙O的直径，P点在AB的延长线上，PM切⊙O于M点，若OA=a，