题目内容
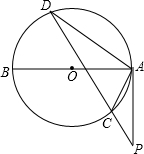（2012•泰宁县质检）已知，如图，AB为⊙O的直径，弦DC延长线上有一点P，∠PAC=∠PDA．（1）求证：PA是⊙O的切线；
（2）若AD=6，∠ACD=60°，求⊙O的半径．
分析：（1）连接BD，根据AB是直径得出∠1+∠2=90°，根据∠1=∠3和∠2=∠PAC求出∠BAP=90°，根据切线的判定推出即可；
（2）求出∠B=∠ACD=60°，求出∠DAB=30°，根据勾股定理求出BD、AB，即可求出答案．
（2）求出∠B=∠ACD=60°，求出∠DAB=30°，根据勾股定理求出BD、AB，即可求出答案．
解答：（1）证明：连接BD，
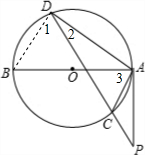
∵AB是⊙O的直径，点D在⊙O上，
∴∠ADB=90°，
∴∠1+∠2=90°，
∵∠1=∠3，∠2=∠PAC，
∴∠3+∠PAC=∠1+∠2，
∴∠BAP=∠3+∠PAC=90°，
又∵OA是⊙O的半径，
∴PA是⊙O的切线．
（2）解：∵∠B=∠ACD=60°，
在Rt△ABD中，∠BAD=30°，AD=6，
设BD=x，AB=2x，
由AD2+BD2=AB2得：x2+62=（2x）2，
解得x=2
，
∴⊙O的半径为2
．
∵AB是⊙O的直径，点D在⊙O上，
∴∠ADB=90°，
∴∠1+∠2=90°，
∵∠1=∠3，∠2=∠PAC，
∴∠3+∠PAC=∠1+∠2，
∴∠BAP=∠3+∠PAC=90°，
又∵OA是⊙O的半径，
∴PA是⊙O的切线．
（2）解：∵∠B=∠ACD=60°，
在Rt△ABD中，∠BAD=30°，AD=6，
设BD=x，AB=2x，
由AD2+BD2=AB2得：x2+62=（2x）2，
解得x=2
| 3 |
∴⊙O的半径为2
| 3 |
点评：本题考查了切线的判定，勾股定理，圆周角定理，三角形的内角和定理等知识点，主要考查学生综合运用行政进行推理和计算的能力，用了方程思想．
练习册系列答案
相关题目
（2012•泰宁县质检）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：