题目内容
 如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆弧上.①若正方形的顶点F也在半圆弧上,则半圆的半径与正方形边长的比是
如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆弧上.①若正方形的顶点F也在半圆弧上,则半圆的半径与正方形边长的比是| 5 |
| 5 |
100
100
.分析:①根据圆和正方形的对称性可知:GH=
DG=
GF,在直角三角形FGH中,利用勾股定理可得HF=
a,从而用含a的代数式表示半圆的半径为
a,正方形边长为2a,所以可求得半圆的半径与正方形边长的比;
②连接EB、AE,OH、OI,可得OHCI是正方形,且边长是4,可设BD=x,AD=y,则BD=BH=x,AD=AI=y,分别利用直角三角形ABC和直角三角形AEB中的勾股定理和相似比作为相等关系列方程求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
②连接EB、AE,OH、OI,可得OHCI是正方形,且边长是4,可设BD=x,AD=y,则BD=BH=x,AD=AI=y,分别利用直角三角形ABC和直角三角形AEB中的勾股定理和相似比作为相等关系列方程求解即可.
解答: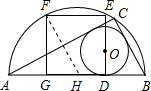 解:①如图,根据圆和正方形的对称性可知:GH=
解:①如图,根据圆和正方形的对称性可知:GH=
DG=
GF,
H为半圆的圆心,不妨设GH=a,则GF=2a,
在直角三角形FGH中,由勾股定理可得HF=
a.由此可得,半圆的半径为
a,正方形边长为2a,
所以半圆的半径与正方形边长的比是
a:2a=
:2;
②连接OI、OJ,可得OICJ是正方形,且边长是4,
设BD=x,AD=y,则BD=BI=x,AD=AJ=y,
在直角三角形ABC中,由勾股定理得(x+4)2+(y+4)2=(x+y)2;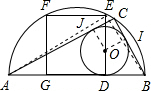
∴8(x+y)+32=2xy,
在直角三角形AEB中,可以证得△ADE∽△EBD∽△ABE,
于是得到ED2=AD•BD,即102=x•y②.
∴正方形DEFG的面积为:100,
故答案为:①
:2,②100.
 解:①如图,根据圆和正方形的对称性可知:GH=
解:①如图,根据圆和正方形的对称性可知:GH=| 1 |
| 2 |
| 1 |
| 2 |
H为半圆的圆心,不妨设GH=a,则GF=2a,
在直角三角形FGH中,由勾股定理可得HF=
| 5 |
| 5 |
所以半圆的半径与正方形边长的比是
| 5 |
| 5 |
②连接OI、OJ,可得OICJ是正方形,且边长是4,
设BD=x,AD=y,则BD=BI=x,AD=AJ=y,
在直角三角形ABC中,由勾股定理得(x+4)2+(y+4)2=(x+y)2;

∴8(x+y)+32=2xy,
在直角三角形AEB中,可以证得△ADE∽△EBD∽△ABE,
于是得到ED2=AD•BD,即102=x•y②.
∴正方形DEFG的面积为:100,
故答案为:①
| 5 |
点评:此题主要考查了圆、三角形、方程等知识,是一道综合性很强的题目,难度偏上,需要正确理解相关知识点及懂得运用方能很好的解答本题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
 (2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )
(2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )
 如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于
如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于