题目内容
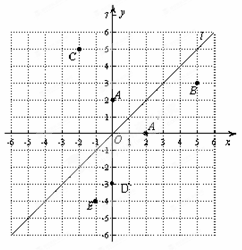
如图,在平面角直角坐标系中,A(-2,0),B(0,3),C(3,0),D(0,2).
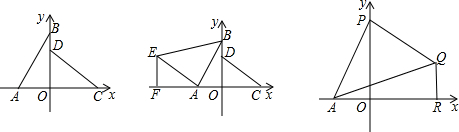
(1)求证:AB=CD且AB⊥CD;
(2)以A为直角顶点在第二象限内作等腰直角三角形ABE,过点E作EF⊥x轴于点F,求点F的坐标;
(3)若点P为y轴正半轴上一动点,以AP为直角边作等腰直角三角形APQ,∠APQ=90°,QR⊥x轴于点R,当点P运动时,OP-QR的值是否发生变化?若不变,求出其值;若变化,请说明理由.
解:(1)证明:延长CD交AB于点E.
∵A(-2,0),B(0,3),C(3,0),D(0,2),
∴OA=OD=2,OB=OC=3.
∵∠AOB=90°,∠DOC=90°,
∴∠AOB=∠DOC.
在△AOB和△DOC中.
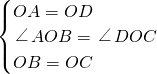 ,
,
∴△AOB≌△DOC(SAS),
∴∠ABO=∠DCO.∠BAO=∠CDO.AB=CD.
∵∠BDE=∠CDO,
∴∠BAO=∠BDE.
∵∠BAO+∠ABO=90°,
∴∠BDE+∠ABO=90°,
∴∠BED=90°,
∴AB⊥CD;
(2)∵三角形ABE是等腰直角三角形,
∴AE=AB,∠EAB=90°,
∴∠FAE+∠BAO=90°.
∵EF⊥x轴,
∴∠EFA=90°,
∴∠AEF+∠FAE=90°,
∴∠AEF=∠OAB.
∵∠AOB=90°,
∴∠EFA=∠AOB.
在△AEF和△BAO中,
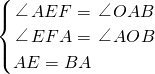 ,
,
∴△AEF≌△BAO(AAS),
∴AF=BO=3,
∴OF=2+3=5,
∴F(0,-5).
答:F的坐标为(0,-5);
(3)OP-QR的值不变.
理由:作QF⊥OP于F,
∴∠PFQ=∠QFO=90°,
∴∠FPQ+∠FQP=90°.
∵三角形APQ是等腰直角三角形,
∴PA=PQ,∠APQ=90°,
∴∠APO+∠OPQ=90°.
∴∠APO=∠PQQF.
∵∠AOP=∠POR=90°,
∴∠AOP=∠PFQ.
在△AOP和△PFQ中,
 ,
,
∴△AOP≌△PFQ(AAS),
∴AO=PF.
∵QR⊥x轴,
∴∠QRA=90°.
∴∠QRA=∠POR=∠QFO=90°,
∴四边形FORQ是矩形,
∴QR=FO.
∴OP-QR=OP-OF=PF,
∴OP-QR=OA.
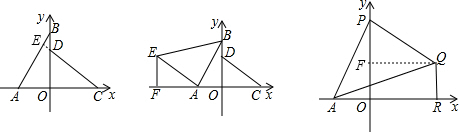
分析:(1)延长CD交AB于点E,根据A(-2,0),B(0,3),C(3,0),D(0,2)可以求出OA=OD=2,OB=OC=3,证明△AOB≌△DOC就可以求出结论;
(2)根据等腰直角三角形的性质可以得出△AEF≌△BAO,就有AF=OB,从而求出F的坐标;
(3)作QF⊥OP于F,根据等腰直角三角形的性质可以得出△AOP≌△PFQ,就有PF=OA,由矩形的性质可以得出QR=OF,就可以得出OP-QR=PF=OA不发生变化.
点评:本题考查了点的坐标的运用,等腰直角三角形的性质的运用,全等三角形的判定与性质的运用,矩形的判定运用的运用,解答时运用全等三角形的性质求解是关键.
∵A(-2,0),B(0,3),C(3,0),D(0,2),
∴OA=OD=2,OB=OC=3.
∵∠AOB=90°,∠DOC=90°,
∴∠AOB=∠DOC.
在△AOB和△DOC中.
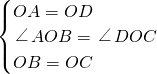 ,
,∴△AOB≌△DOC(SAS),
∴∠ABO=∠DCO.∠BAO=∠CDO.AB=CD.
∵∠BDE=∠CDO,
∴∠BAO=∠BDE.
∵∠BAO+∠ABO=90°,
∴∠BDE+∠ABO=90°,
∴∠BED=90°,
∴AB⊥CD;
(2)∵三角形ABE是等腰直角三角形,
∴AE=AB,∠EAB=90°,
∴∠FAE+∠BAO=90°.
∵EF⊥x轴,
∴∠EFA=90°,
∴∠AEF+∠FAE=90°,
∴∠AEF=∠OAB.
∵∠AOB=90°,
∴∠EFA=∠AOB.
在△AEF和△BAO中,
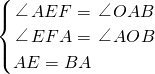 ,
,∴△AEF≌△BAO(AAS),
∴AF=BO=3,
∴OF=2+3=5,
∴F(0,-5).
答:F的坐标为(0,-5);
(3)OP-QR的值不变.
理由:作QF⊥OP于F,
∴∠PFQ=∠QFO=90°,
∴∠FPQ+∠FQP=90°.
∵三角形APQ是等腰直角三角形,
∴PA=PQ,∠APQ=90°,
∴∠APO+∠OPQ=90°.
∴∠APO=∠PQQF.
∵∠AOP=∠POR=90°,
∴∠AOP=∠PFQ.
在△AOP和△PFQ中,
 ,
,∴△AOP≌△PFQ(AAS),
∴AO=PF.
∵QR⊥x轴,
∴∠QRA=90°.
∴∠QRA=∠POR=∠QFO=90°,
∴四边形FORQ是矩形,
∴QR=FO.
∴OP-QR=OP-OF=PF,
∴OP-QR=OA.

分析:(1)延长CD交AB于点E,根据A(-2,0),B(0,3),C(3,0),D(0,2)可以求出OA=OD=2,OB=OC=3,证明△AOB≌△DOC就可以求出结论;
(2)根据等腰直角三角形的性质可以得出△AEF≌△BAO,就有AF=OB,从而求出F的坐标;
(3)作QF⊥OP于F,根据等腰直角三角形的性质可以得出△AOP≌△PFQ,就有PF=OA,由矩形的性质可以得出QR=OF,就可以得出OP-QR=PF=OA不发生变化.
点评:本题考查了点的坐标的运用,等腰直角三角形的性质的运用,全等三角形的判定与性质的运用,矩形的判定运用的运用,解答时运用全等三角形的性质求解是关键.

练习册系列答案
相关题目