摘要：28．已知:如图.函数的图象与x轴相交于点A.与函数的图象相交于点P． (1)求点P的坐标． (2)请判断的形状并说明理由． (3)动点E从原点O出发.以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O.A重合).过点E分别作EF⊥x轴于F.EB⊥y轴于B．设运动t秒时.矩形EBOF与△OPA重叠部分的面积为S． 求:① S与t之间的函数关系式． ② 当t为何值时.S最大.并求S的最大值．
网址：http://m.1010jiajiao.com/timu3_id_487462[举报]
已知：如图，函数y=-x+2的图象与x轴、y轴分别交于点A、B，一直线
经过点C（1，0），将△AOB的面积分成相等的两部分。
经过点C（1，0），将△AOB的面积分成相等的两部分。
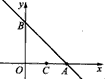
（1）求直线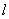
的函数解析式；
（2）若直线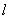
将△AOB的面积分成1：3两部分，求直线
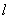的函数解析式。
查看习题详情和答案>>
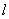的函数解析式； （2）若直线
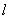将△AOB的面积分成1：3两部分，求直线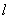的函数解析式。
已知：如图，二次函数y=x2-4的图象与x轴交于A、B两点（点A在点B的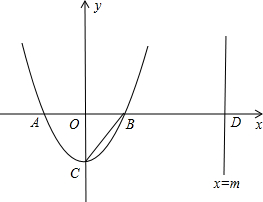
左边），与y轴交于点C．直线x=m（m＞2）与x轴交于点D．
（1）求A、B、C三点的坐标；
（2）在直线x=m（m＞2）上有一点P（点P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求P点的坐标（用含m的代数式表示）；
（3）在（2）成立的条件下，试问：抛物线y=x2-4上是否存在一点Q，使得四边形ABPQ为平行四边形？如果存在这样的点Q，请求出m的值；如果不存在，请简要说明理由． 查看习题详情和答案>>
左边），与y轴交于点C．直线x=m（m＞2）与x轴交于点D．（1）求A、B、C三点的坐标；
（2）在直线x=m（m＞2）上有一点P（点P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求P点的坐标（用含m的代数式表示）；
（3）在（2）成立的条件下，试问：抛物线y=x2-4上是否存在一点Q，使得四边形ABPQ为平行四边形？如果存在这样的点Q，请求出m的值；如果不存在，请简要说明理由． 查看习题详情和答案>>
已知：如图，二次函数y=2x2-2的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，直线x=m（m＞1）与x轴交于点D．
（1）求A、B、C三点的坐标；
（2）在直线x=m（m＞1）上有一点P（点P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求P点坐标（用含m的代数式表示）；
（3）在（2）成立的条件下，试问：抛物线y=2x2-2上是否存在一点Q，使得四边形A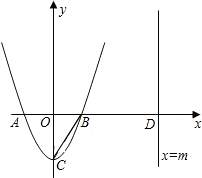
BPQ为平行四边形？如果存在这样的点Q，请求出m的值；如果不存在，请简要说明理由．
查看习题详情和答案>>
（1）求A、B、C三点的坐标；
（2）在直线x=m（m＞1）上有一点P（点P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求P点坐标（用含m的代数式表示）；
（3）在（2）成立的条件下，试问：抛物线y=2x2-2上是否存在一点Q，使得四边形A
BPQ为平行四边形？如果存在这样的点Q，请求出m的值；如果不存在，请简要说明理由．
查看习题详情和答案>>
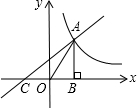已知：如图，已知一次函数y=x+1的图象与反比例函数
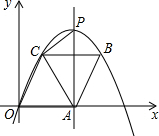、C在这条抛物线上，如果四边形OABC是菱形，