题目内容
已知:如图,经过原点的抛物线的顶点为P,这条抛物线的对称轴x=2与x轴相交于点A,点B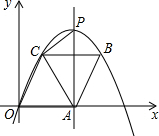 、C在这条抛物线上,如果四边形OABC是菱形,
、C在这条抛物线上,如果四边形OABC是菱形,(1)求∠AOC的度数;
(2)求以这条抛物线为图象的二次函数的解析式;
(3)试探究:△ACP是否为直角三角形?并证明你的猜想.
分析:(1)由四边形ABCD是菱形,可得BC∥AO,又由PA⊥AO,然后根据抛物线的对称性可得:AC=AB则可证得△AOC是等边三角形,即可求得∠AOC的度数;
(2)由(1)即可求得点C与D的坐标,即可设所求二次函数的解析式为y=ax2+bx,然后利用待定系数法即可求得此二次函数的解析式;
(3)由(1)即可求得顶点P的坐标即可求得PA,PC,AC的长,然后由勾股定理的逆定理,即可判定△ACP是直角三角形.
(2)由(1)即可求得点C与D的坐标,即可设所求二次函数的解析式为y=ax2+bx,然后利用待定系数法即可求得此二次函数的解析式;
(3)由(1)即可求得顶点P的坐标即可求得PA,PC,AC的长,然后由勾股定理的逆定理,即可判定△ACP是直角三角形.
解答:解:(1)∵四边形ABCD是菱形,
∴BC∥AO.
∵PA⊥AO,
∴PA⊥BC.(1分)
由抛物线的对称性可得:AC=AB.(1分)
∴AC=AO=OC.
∴∠AOC=60°.(1分)
(2)由(1)可得,点C的坐标为(1,
),点B的坐标为(3,
).(2分)
设所求二次函数的解析式为y=ax2+bx.
∵这个函数的图象经过点B和点C,
∴
,
解得
,(1分)
∴所求的二次函数的解析式为:y=-
x2+
x.(1分)
(3)是.(1分)
证明:由条件得顶点P的坐标为(2,
),(1分)
∴PA=
,PC=
,AC=2.
∴PA2=PC2+AC2.(1分)
∴△ACP是直角三角形.
∴BC∥AO.
∵PA⊥AO,
∴PA⊥BC.(1分)
由抛物线的对称性可得:AC=AB.(1分)
∴AC=AO=OC.
∴∠AOC=60°.(1分)
(2)由(1)可得,点C的坐标为(1,
| 3 |
| 3 |
设所求二次函数的解析式为y=ax2+bx.
∵这个函数的图象经过点B和点C,
∴
|
解得
|
∴所求的二次函数的解析式为:y=-
| ||
| 3 |
4
| ||
| 3 |
(3)是.(1分)
证明:由条件得顶点P的坐标为(2,
| 4 |
| 3 |
| 3 |
∴PA=
4
| ||
| 3 |
2
| ||
| 3 |
∴PA2=PC2+AC2.(1分)
∴△ACP是直角三角形.
点评:此题考查了待定系数法求函数的解析式,菱形的性质,勾股定理的逆定理的应用等知识.此题综合性较强,难度适中,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
相关题目
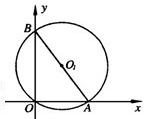 23、已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A(3,0)、B(0,4).设△BOA的内切圆的直径为d,则d+AB的值为
23、已知:如图,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A(3,0)、B(0,4).设△BOA的内切圆的直径为d,则d+AB的值为 原点O及A、B两点.
原点O及A、B两点.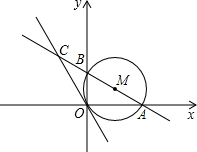 已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(
已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(