摘要: 图形旋转的定义:把一个图形 的图形变换.叫做旋转. 叫做旋转中心. 叫做旋转角.
网址:http://m.1010jiajiao.com/timu3_id_486088[举报]
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
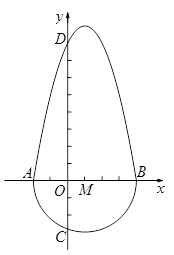
(1)请你直接写出“蛋圆”抛物线部分的解析式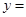 ,自变量的取值范围是 ;
,自变量的取值范围是 ;
(2)请你求出过点C的“蛋圆”切线与x轴的交点坐标;
(3)求经过点D的“蛋圆”切线的解析式.

(1)请你直接写出“蛋圆”抛物线部分的解析式
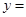 ,自变量的取值范围是 ;
,自变量的取值范围是 ;(2)请你求出过点C的“蛋圆”切线与x轴的交点坐标;
(3)求经过点D的“蛋圆”切线的解析式.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
(1)请你直接写出“蛋圆”抛物线部分的解析式 ,自变量的取值范围是 ;
,自变量的取值范围是 ;
(2)请你求出过点C的“蛋圆”切线与x轴的交点坐标;
(3)求经过点D的“蛋圆”切线的解析式.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆的圆心M的坐标为(1,0),半圆半径为3.
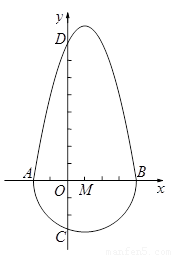
(1)请你直接写出“蛋圆”抛物线部分的解析式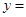 ,自变量的取值范围是
;
,自变量的取值范围是
;
(2)请你求出过点C的“蛋圆”切线与x轴的交点坐标;
(3)求经过点D的“蛋圆”切线的解析式.
查看习题详情和答案>>
在旋转的定义下,如果旋转一定角度后能与自身重合的图形叫做旋转对称图形.如正方形绕它的中心旋转90°角后能与自身重合,所以正方形是旋转对称图形.
(1
)判断下列说法是否正确(在相应括号内填上撌菙或摲駭):①等腰梯形是旋转对称图形,它有一个旋转角为180°;( )
②长方形是旋转对称图形,它有一个旋转角为180°.( )
(2
)填空:下列图形中,是旋转对称图形,且有一个旋转角为120°的是_____(只填序号).①等边三角形;②正方形;③正六边形;④正八边形.(3
)写出两个多边形,它们都是旋转对称图形,都有一个旋转角为72°,并且分别满足下列条件:①是轴对称图形,但不是中心对称图形;②既是轴对称图形,又是中心对称图形. 查看习题详情和答案>>