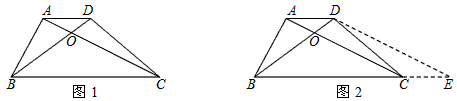网址:http://m.1010jiajiao.com/timu3_id_485404[举报]
如图,射线BN、AM都垂直于线段AB,E为AM上一动点, ⊥
⊥ 于F,交BN于C,
于F,交BN于C, ⊥
⊥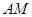 于
于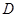 ,连接BD.
,连接BD.
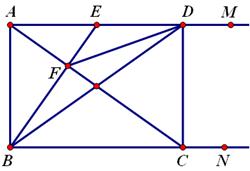
⑴求证:  ;
;
⑵当 为
为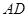 的中点时,求证:
的中点时,求证:
 ;
;
⑶设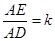 ,请探究出使
,请探究出使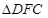 为
为
等腰三角形的实数 的值.
的值.
【解析】(1)中利用 ⊥
⊥
得到直角三角形AEF相似于三角形ABE,然后得到结论。
(2)中,
由⑴有 ,因为
,因为 为
为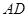 的中点,所以
的中点,所以
则可以得到

从而的得到角相等
(3)中,设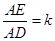 ,当使
,当使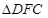 为
为
等腰三角形时,需要考查谁是腰,分类讨论得到
①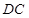 为腰,且
为腰,且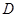 为顶角顶点;
为顶角顶点;
②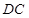 为腰,且
为腰,且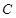 为顶角顶点;
为顶角顶点;
③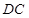 为底.
为底.
①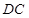 为腰,且
为腰,且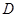 为顶角顶点;
为顶角顶点;
解得答案为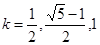
查看习题详情和答案>>
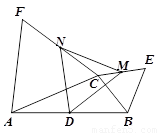
如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形, M、N分别是CE、CF的中点.
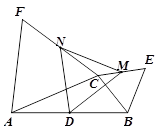
1.求证:△DMN是等边三角形;
2.连接EF,Q是EF中点,CP⊥EF于点P. 求证:DP=DQ.
同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考:
小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.
查看习题详情和答案>>
如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形, M、N分别是CE、CF的中点.
1.求证:△DMN是等边三角形;
2.连接EF,Q是EF中点,CP⊥EF于点P. 求证:DP=DQ.
同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考:
小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.
查看习题详情和答案>>
小伟遇到这样一个问题:如图1,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,若梯形ABCD的面积为1,试求以AC、BD、AD+BC的长度为三边长的三角形的面积;
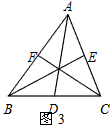
小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可,他先后尝试了翻折、旋转、平移的方法,发现通过平移可以解决这个问题,他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC、BD、AD+BC的长度为三边长的三角形(如图2),请你回答:图2中△BDE的面积等于_____;
参考小伟同学的思考问题的方法,解决下列问题:
如图3,△ABC的三条中线分别为AD、BE、CF。
(1)在图3中利用图形变换画出并指明以AD、BE、CF 的长度为三边长的一个三角形(保留画图痕迹);
(2)若△ABC的面积为1,则以AD、BE、CF的长度为三边长的三角形的面积等于_____。