题目内容
如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形, M、N分别是CE、CF的中点.
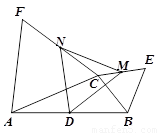
1.求证:△DMN是等边三角形;
2.连接EF,Q是EF中点,CP⊥EF于点P. 求证:DP=DQ.
同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考:
小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.
【答案】
1.取AC的中点G,连接NG、DG.

∴DG=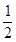 BC,DG∥BC;△NGC是等边三角形.
BC,DG∥BC;△NGC是等边三角形.
∴NG = NC,DG = CM.
∵∠1 + ∠2 = 180º,
∴∠NGD + ∠2 = 240º.
∵∠2 + ∠3 = 240º,
∴∠NGD =∠3.
∴△NGD≌△NCM .
∴ND = NM ,∠GND =∠CNM.
∴∠DNM =∠GNC = 60º.
∴△DMN是等边三角形.
2.连接QN、PM.
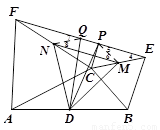
∴QN =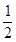 CE=
PM.
CE=
PM.
Rt△CPE中,PM =EM,∴∠4= ∠5.
∵MN∥EF,∴∠5= ∠6,∠7= ∠8.
∵NQ∥CE,∴∠7= ∠4.
∴∠6= ∠8.
∴∠QND= ∠PMD.
∴△QND≌△PMD.
∴DQ= DP.
【解析】
1.先证出NG = NC,DG = CM,再证出△NGD≌△NCM,得出△DMN是等边三角形;
2.根据题意得出QN =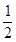 CE=
PM,然后证明△QND≌△PMD,从而得出DQ= DP.
CE=
PM,然后证明△QND≌△PMD,从而得出DQ= DP.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( )
8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( ) 13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于
13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于 如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( )
如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( ) 如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( )
如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( ) 如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=
如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=