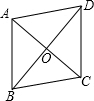
摘要:4.四边形:对平行四边形.矩形.菱形.正方形.等腰梯形的性质与判定.了解多边形的内角和与外角和公式.正多边形的概念.平面的密铺及其简单设计等.
网址:http://m.1010jiajiao.com/timu3_id_485286[举报]
将平行四边形、矩形、菱形、正方形、直角梯形、等腰梯形分成下列两组:
①平行四边形、直角梯形、等腰样形;
②矩形、菱形、正方形,其分类的依据是
- A.对角线互相平分
- B.属于轴对称图形或中心对称图形
- C.内角和相等
- D.既是中心对称图形又是轴对称图形
将平行四边形、矩形、菱形、正方形、直角梯形、等腰梯形分成下列两组:①平行四边形、直角梯形、等腰样形;②矩形、菱形、正方形,其分类的依据是
[ ]
A.对角线互相平分
B.属于轴对称图形或中心对称图形
C.内角和相等
D.既是中心对称图形又是轴对称图形
查看习题详情和答案>>
矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形.正方形不仅是特殊的平行四边形,而且是邻边相等的特殊矩形,也是有一个角是直角的特殊菱形.因此,我们可以利用矩形、菱形的性质来研究正方形的有关问题,回答下列问题:
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系图中:
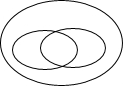
(2)要证明一个四边形是正方形,可以先证明四边形是矩形,再证明这个矩形的 相等;或者先证明四边形是菱形,再证明这个菱形有一角是 .
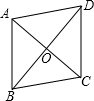
(3)如下图菱形ABCD,某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=
a2,对此结论,你认为是否正确?若正确,请给予证明;若不正确,举出一个反例来说明.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系图中:

(2)要证明一个四边形是正方形,可以先证明四边形是矩形,再证明这个矩形的
(3)如下图菱形ABCD,某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=
| 1 | 2 |
 查看习题详情和答案>>
查看习题详情和答案>>
矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题:
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的 相等;或者先证明四边形是菱形,在证明这个菱形有一个角是 .
(3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2,对此结论,你认为是否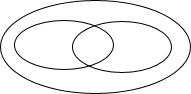 正确?若正确,请说明理由;若不正确,请举出一个反例说明.
查看习题详情和答案>>
正确?若正确,请说明理由;若不正确,请举出一个反例说明.
查看习题详情和答案>>
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的
(3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2,对此结论,你认为是否
 正确?若正确,请说明理由;若不正确,请举出一个反例说明.
查看习题详情和答案>>
正确?若正确,请说明理由;若不正确,请举出一个反例说明.
查看习题详情和答案>>
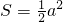 ,对此结论,你认为是否正确?若正确,请给予证明;若不正确,举出一个反例来说明.
,对此结论,你认为是否正确?若正确,请给予证明;若不正确,举出一个反例来说明.