摘要:4.理解比例的概念和基本性质.会解简单的比例问题(对合分比定理和等比定理不作教学要求)
网址:http://m.1010jiajiao.com/timu3_id_484487[举报]
阅读理解题:
我们学习了二次根式的概念及其基本性质,又学习了二次根式的乘法运算法则,下面我们再来思考下面的问题:
(1)计算:
•
=
•
=
•
=
=
=
.
试一试:化简:①
=
=
;②
=
=
;
(2)计算:(2﹢
)(2-
)=
﹢
)(
-
)=
-3)(
+3
+3)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简:
.
查看习题详情和答案>>
我们学习了二次根式的概念及其基本性质,又学习了二次根式的乘法运算法则,下面我们再来思考下面的问题:
(1)计算:
| 2 |
| 2 |
2
2
;| 3 |
| 3 |
3
3
;| 12 |
| 3 |
6
6
;显然将一个二次根式乘以一个适当的二次根式后结果不再含有根号.因此利用这个性质结合二次根式除法法则、分式基本性质可以化去分母中的根号,使分母中不再含有根号,如:
| ||
|
| ||||
|
| ||
| 3 |
试一试:化简:①
| 1 | ||
|
1•
| ||||
|
1•
| ||||
|
| ||
| 6 |
| ||
| 6 |
| ||
|
| ||||
|
| ||||
|
| ||
| 3 |
| ||
| 3 |
(2)计算:(2﹢
| 3 |
| 3 |
1
1
;(| 6 |
| 2 |
| 6 |
| 2 |
4
4
;同样发现相乘的积不再含有根号.想一想:(| 7 |
| 7 |
| 7 |
| 1 | ||
|
阅读理解题:
我们学习了二次根式的概念及其基本性质,又学习了二次根式的乘法运算法则,下面我们再来思考下面的问题:
(1)计算: •
• =______;
=______; •
• =______;
=______; •
• =______;显然将一个二次根式乘以一个适当的二次根式后结果不再含有根号.因此利用这个性质结合二次根式除法法则、分式基本性质可以化去分母中的根号,使分母中不再含有根号,如:
=______;显然将一个二次根式乘以一个适当的二次根式后结果不再含有根号.因此利用这个性质结合二次根式除法法则、分式基本性质可以化去分母中的根号,使分母中不再含有根号,如: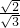 =
=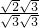 =
= .
.
试一试:化简:①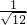 =______=______;②
=______=______;②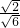 =______=______;
=______=______;
(2)计算:(2﹢ )(2-
)(2- )=______;(
)=______;( ﹢
﹢ )(
)( -
- )=______;同样发现相乘的积不再含有根号.想一想:(
)=______;同样发现相乘的积不再含有根号.想一想:( -3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简:
-3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简: .
.
查看习题详情和答案>>
我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
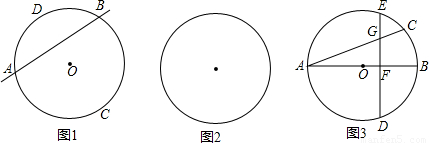
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是
的中点,弦DE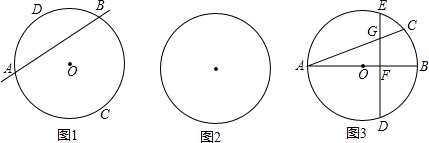 ⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
查看习题详情和答案>>
⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
查看习题详情和答案>>
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是
 | ABC |
 ⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
查看习题详情和答案>>
⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
查看习题详情和答案>>
我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是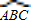 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是
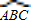 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由. 查看习题详情和答案>>
查看习题详情和答案>>
我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是
 的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由. 查看习题详情和答案>>
查看习题详情和答案>>