题目内容
阅读理解题:
我们学习了二次根式的概念及其基本性质,又学习了二次根式的乘法运算法则,下面我们再来思考下面的问题:
(1)计算:
•
=
•
=
•
=
=
=
.
试一试:化简:①
=
=
;②
=
=
;
(2)计算:(2﹢
)(2-
)=
﹢
)(
-
)=
-3)(
+3
+3)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简:
.
我们学习了二次根式的概念及其基本性质,又学习了二次根式的乘法运算法则,下面我们再来思考下面的问题:
(1)计算:
| 2 |
| 2 |
2
2
;| 3 |
| 3 |
3
3
;| 12 |
| 3 |
6
6
;显然将一个二次根式乘以一个适当的二次根式后结果不再含有根号.因此利用这个性质结合二次根式除法法则、分式基本性质可以化去分母中的根号,使分母中不再含有根号,如:
| ||
|
| ||||
|
| ||
| 3 |
试一试:化简:①
| 1 | ||
|
1•
| ||||
|
1•
| ||||
|
| ||
| 6 |
| ||
| 6 |
| ||
|
| ||||
|
| ||||
|
| ||
| 3 |
| ||
| 3 |
(2)计算:(2﹢
| 3 |
| 3 |
1
1
;(| 6 |
| 2 |
| 6 |
| 2 |
4
4
;同样发现相乘的积不再含有根号.想一想:(| 7 |
| 7 |
| 7 |
| 1 | ||
|
分析:(1)计算:根据二次根式的乘法法则进行计算;
化简:分母有理化即可;
(2)计算:利用平方差公式进行计算;
化简:分母有理化:将一个二次根式乘以一个适当的二次根式后结果不再含有根号.
化简:分母有理化即可;
(2)计算:利用平方差公式进行计算;
化简:分母有理化:将一个二次根式乘以一个适当的二次根式后结果不再含有根号.
解答:解:(1)计算:
•
=2;
•
=3;
•
=6;
试一试:化简:①
=
=
;②
=
=
;
(2)计算:(2﹢
)(2-
)=1;(
﹢
)(
-
)=4;
想一想:(
-3)(
+3)=7-3=4,所以,(
-3)(
+3)使其结果不再含有根号;
化简:
解:
=
=(
+2).
| 2 |
| 2 |
| 3 |
| 3 |
| 12 |
| 3 |
试一试:化简:①
| 1 | ||
|
1•
| ||||
|
| ||
| 6 |
| ||
|
| ||||
|
| ||
| 3 |
(2)计算:(2﹢
| 3 |
| 3 |
| 6 |
| 2 |
| 6 |
| 2 |
想一想:(
| 7 |
| 7 |
| 7 |
| 7 |
化简:
| 1 | ||
|
解:
| 1 | ||
|
1•(
| ||||
(
|
| 5 |
点评:本题考查了分母有理化.分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
相关题目
 •
• •
• •
•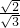 =
=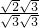 =
= .
.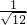 =______=______;②
=______=______;②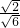 =______=______;
=______=______; ﹢
﹢ -3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简:
-3)(______)使其结果不再含有根号;同样请你仿照(1)的方法将下列二次根式化简: .
.