Question

如图（14），已知 ，，现以A点为位似中心，相似比为9:4，将OB向右侧放大，B点的对应点为C．

1.求C点坐标及直线BC的解析式;

2.一抛物线经过B、C两点，且顶点落在x轴正半轴上，求该抛物线的解析式并画出函数图象;

3.现将直线BC绕B点旋转与抛物线相交于另一点P，请找出抛物线上所有满足到直线AB距离为的点P．

 

Answer 1

【答案】

 

1.过C点向x轴作垂线，垂足为D，由位似图形性质可知：

△ABO∽△ACD， ∴．

由已知，可知： ．

∴．∴C点坐标为．………………2分

直线BC的解析是为：

化简得：    ……………………………… 3分

2.设抛物线解析式为，由题意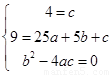得： ，解得： ,

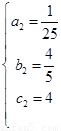
∴解得抛物线解析式为或．

又∵的顶点在x轴负半轴上，不合题意，故舍去．

∴满足条件的抛物线解析式为·················· 5分

（画出函数图象）  7分

3.将直线BC绕B点旋转与抛物线相交与另一点P，设P到 直线AB的距离为h，

故P点应在与直线AB平行，且相距的上下两条平行直线和上．······ 8分

由平行线的性质可得：两条平行直线与y轴的交点到直线BC的距离也为．

如图，设与y轴交于E点，过E作EF⊥BC于F点，

在Rt△BEF中，，

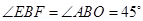∴．∴可以求得直线与y轴交点坐标为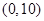············· 10分

同理可求得直线与y轴交点坐标为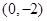·················· 11分

∴两直线解析式；．

根据题意列出方程组： ⑴；⑵

∴解得：；；；

∴满足条件的点P有四个，它们分别是，，，·· 13分

【解析】（1）利用相似及相似比，可得到C的坐标．把A，B代入一次函数解析式即可求得解析式的坐标．

（2）顶点落在x轴正半轴上说明此函数解析式与x轴有一个交点，那么△=0，再把B，C两点即可．

（3）到直线AB的距离为3 的直线有两条，可求出这两条直线解析式，和二次函数解析式组成方程组，求得点P坐标