摘要： 在平面直角坐标系中给定以下五个点． (1)请从五点中任选三点.求一条以平行于轴的直线为对称轴的抛物线的解析式, (2)求该抛物线的顶点坐标和对称轴.并画出草图, (3)已知点在抛物线的对称轴上.直线过点且垂直于对称轴．验证:以为圆心.为半径的圆与直线相切．请你进一步验证.以抛物线上的点为圆心为半径的圆也与直线相切．由此你能猜想到怎样的结论． 25．解:(1)设抛物线的解析式为. 且过点. 由在H ． 则．········································································································ 得方程组. 解得． 抛物线的解析式为················ (2)由············· 得顶点坐标为.对称轴为．·········· (3)①连结.过点作直线的垂线.垂足为. 则． 在中... . . 以点为圆心.为半径的与直线相切．····························· ②连结过点作直线的垂线.垂足为．过点作垂足为. 则． 在中..． ． 以点为圆心为半径的与直线相切．································ ③以抛物线上任意一点为圆心.以为半径的圆与直线相切．·····
网址：http://m.1010jiajiao.com/timu3_id_480111[举报]
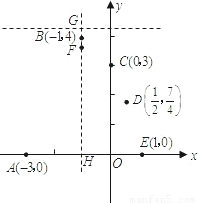
在平面直角坐标系中给定以下五个点A（-3，0），B（-1，4），C（0，3），D（| 1 |
| 2 |
| 7 |
| 4 |
（1）请从五点中任选三点，求一条以平行于y轴的直线为对称轴的抛物线的解析式；
（2）求该抛物线的顶点坐标和对称轴，并画出草图；
（3）已知点F（-1，
| 15 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
| 17 |
| 4 |
在平面直角坐标系中给定以下五个点A（-2，0）、B（1，0）、C（4，0）、D（-2，
）、E（0，-6），在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点．玩摸球游戏，每次摸三个球，摸一次，三球代表的点恰好能确定一条抛物线（对称轴平行于y轴）的概率是（ ）
| 9 |
| 2 |
在平面直角坐标系中给定以下五个点A（-2，0）、B（1，0）、C（4，0）、D（-2，
）、E（0，-6），从这五个点中选取三点，使经过三点的抛物线满足以y轴的平行线为对称轴．我们约定经过A、B、E三点的抛物线表示为抛物线ABE．
（1）符合条件的抛物线共有多少条不求解析式，请用约定的方法一一表示出来；
（2）在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点，玩摸球游戏，每次摸三个球．请问：摸一次，三球代表的点恰好能确定一条符合条件的抛物线的概率是多少？
（3）小强、小亮用上面的五球玩游戏，若符合要求的抛物线．开口向上，小强可以得1分；若抛物线开口向下小亮得5分，你认为这个游戏谁获胜的可能性大一些？说说你的理由． 查看习题详情和答案>>
| 9 | 2 |
（1）符合条件的抛物线共有多少条不求解析式，请用约定的方法一一表示出来；
（2）在五个形状、颜色、质量完全相同的乒乓球上标上A、B、C、D、E代表以上五个点，玩摸球游戏，每次摸三个球．请问：摸一次，三球代表的点恰好能确定一条符合条件的抛物线的概率是多少？
（3）小强、小亮用上面的五球玩游戏，若符合要求的抛物线．开口向上，小强可以得1分；若抛物线开口向下小亮得5分，你认为这个游戏谁获胜的可能性大一些？说说你的理由． 查看习题详情和答案>>
，
），E（1，0）．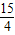
）在抛物线的对称轴上，直线y=
过点G（-1，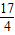
）且垂直于对称轴．验证：以E（1，0）为圆心，EF为半径的圆与直线y=
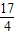相切．请你进一步验证，以抛物线上的点D（
，
）为圆心DF为半径的圆也与直线y=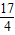
相切．由此你能猜想到怎样的结论．