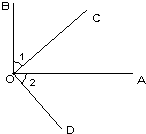
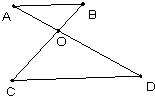
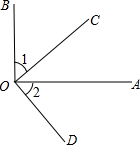摘要:20.(1)解:∵OA=OB ∴∠OAB=∠OBA=40° ∴∠AOB=180°-=100° (2)证明:连结OC并延长交圆O于E.连结BE ∵∠CEB=∠CAB. 而CB=CA ∴∠CEB=∠CBA. 而CE为圆O之直径 ∴∠CEB+∠ECB=90° ∴∠CBA+∠ECB=90° 又AB∥CD ∴∠BCD=∠CBA ∴∠BCD+∠ECB=90°.即∠ECD=90°. 而C在圆O上 ∴CD为圆O之切线
网址:http://m.1010jiajiao.com/timu3_id_479073[举报]
已知(如图)OA⊥OB,∠AOC=∠BOD,请把判断OC⊥OD的推理过程补充完整.
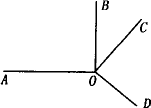
∵OA⊥OB
∴________=90°( )
∵________=∠AOC-∠BOC,
________=∠BOD-∠BOC
∵∠AOC=∠BOD
∴________=________(等量代换)
∴________=90°
∴OC⊥OD( )