摘要:[答案](1)EF=EB.证明:如图.以E为圆心.以EA为半径画弧交直线m于点M,连结EM. ∴EM=EA, ∴∠EMA=∠EAM. ∵BC=Kab,k=1.∴BC=AB. ∴∠CAB=∠ACB. ∵m∥n.∴∠MAC=∠ACB, ∠FAB=∠ABC. ∴∠MAC=∠CAB. ∴∠CAB=∠EMA. ∵∠BEF=∠ABC, ∴∠BEF=∠FAB. ∵∠AHF=∠EHB, ∴∠AFE=∠ABE. ∴△AEB≌△MEF. ∴EF=EB. 探索思路:如上图.∵BC=Kab,k=1.∴BC=AB. ∴∠CAB=∠ACB. ∵m∥n.∴∠MAC=∠ACB. 添加条件:∠ABC=90°. 证明:如图.在直线m上截取AM=AB.连结ME. ∵BC=kAB,k=1.∴BC=AB.∵∠ABC=90°, ∴∠CAB=∠ACB=45°, ∵m∥n.∴∠MAE=∠ACB=∠CAB=45°, ∠FAB=90°. ∵AE=AE, ∴△MAE≌△ABE. ∴EM=EB, ∠AME=∠ABE. ∵∠BEF=∠ABC=90°, ∴∠FAB+∠BEF=180°. ∴∠ABE+∠EFA=180°,又∵∠AME+∠EMF=180°, ∴∠EMF=∠EFA. ∴EM=EF. ∴EF=EB. (2)EF=EB. 说明:如图.过点E作EM⊥m.EN⊥AB,垂足为M.N. ∴∠EMF=∠ENA=∠ENB=90°. ∵m∥n.∠ABC=90°, ∴∠MAB=90°. ∴四边形MENA为矩形.∴ME=NA, ∠MEN=90°. ∵∠BEF=∠ABC=90°. ∴∠MEF=∠NEB. ∴△MEF∽△NEB. ∴∴ 在Rt△ANE和Rt△ABC中.tan∠BAC=. ∴EF=EB.
网址:http://m.1010jiajiao.com/timu3_id_478886[举报]
已知:如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,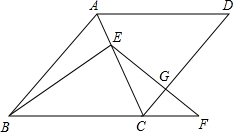 EF与CD相交于点G.
EF与CD相交于点G.
(1)求证:EG•GF=CG•GD;
(2)连接DF,如果EF⊥CD,那么∠FDC与∠ADC之间有怎样的数量关系?证明你所得到的结论. 查看习题详情和答案>>
 EF与CD相交于点G.
EF与CD相交于点G.(1)求证:EG•GF=CG•GD;
(2)连接DF,如果EF⊥CD,那么∠FDC与∠ADC之间有怎样的数量关系?证明你所得到的结论. 查看习题详情和答案>>
(2010•静安区二模)已知:如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G.
(1)求证:EG•GF=CG•GD;
(2)连接DF,如果EF⊥CD,那么∠FDC与∠ADC之间有怎样的数量关系?证明你所得到的结论.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求证:EG•GF=CG•GD;
(2)连接DF,如果EF⊥CD,那么∠FDC与∠ADC之间有怎样的数量关系?证明你所得到的结论.
 查看习题详情和答案>>
查看习题详情和答案>>
填写证明的理由.
已知:如图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG.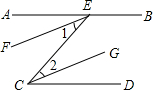
证明:∵AB∥CD(已知)
∴∠AEC=∠DCE ( )
又∵EF平分∠AEC (已知)
∴∠1=
∠AEC ( )
同理∠2=
∠DCE,∴∠1=∠2
∴EF∥CG ( )
查看习题详情和答案>>
已知:如图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG.

证明:∵AB∥CD(已知)
∴∠AEC=∠DCE (
又∵EF平分∠AEC (已知)
∴∠1=
| 1 |
| 2 |
同理∠2=
| 1 |
| 2 |
∴EF∥CG (
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN= 时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
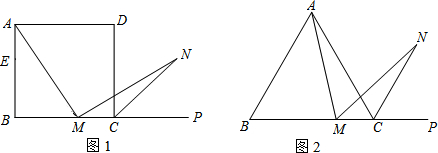 查看习题详情和答案>>
查看习题详情和答案>>
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连接ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,请你作出猜想:当∠AMN=
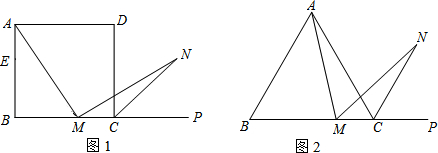 查看习题详情和答案>>
查看习题详情和答案>>
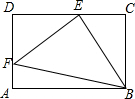 如图,矩形ABCD中,EF⊥EB,EF=EB,ABCD周长为22cm,CE=3cm,求:DE的长.
如图,矩形ABCD中,EF⊥EB,EF=EB,ABCD周长为22cm,CE=3cm,求:DE的长.