题目内容
已知:如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,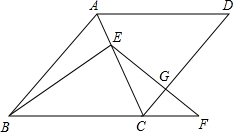 EF与CD相交于点G.
EF与CD相交于点G.(1)求证:EG•GF=CG•GD;
(2)连接DF,如果EF⊥CD,那么∠FDC与∠ADC之间有怎样的数量关系?证明你所得到的结论.
分析:(1)连接ED,首先证明△BCE≌△DCE,得∠EDC=∠EBC;利用此条件再证明∠DGE∽△FGC,即可得到EG•GF=CG•GD.
(2)利用第一题的结论,可证明△DGE∽△FGC,再利用三角形内角外角关系即可得到∠ADC与∠FDC的关系.
(2)利用第一题的结论,可证明△DGE∽△FGC,再利用三角形内角外角关系即可得到∠ADC与∠FDC的关系.
解答: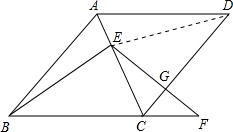 (1)证明:连接ED,(1分)
(1)证明:连接ED,(1分)
∵点E在菱形ABCD的对角线AC上,
∴∠ECB=∠ECD,(2分)
∵BC=CD,CE=CE,
∴△BCE≌△DCE;(3分)
∴∠EDC=∠EBC,(4分)
∵EB=EF,
∴∠EBC=∠EFC;(5分)
∴∠EDC=∠EFC;(6分)
∵∠DGE=∠FGC,
∴△DGE∽△FGC;(7分)
∴
=
,∴EG•GF=CG•GD;(8分)
(2)解:∠ADC=2∠FDC.(9分)
证明如下:∵
=
,∠DGF=∠EGC,
∴△CGE∽△FGD;(10分)
∵EF⊥CD,DA=DC,
∴∠DAC=∠DCA=∠DFG=90°-∠FDC,(11分)
∴∠ADC=180°-2∠DAC=180°-2(90°-∠FDC)=2∠FDC.(12分)
 (1)证明:连接ED,(1分)
(1)证明:连接ED,(1分)∵点E在菱形ABCD的对角线AC上,
∴∠ECB=∠ECD,(2分)
∵BC=CD,CE=CE,
∴△BCE≌△DCE;(3分)
∴∠EDC=∠EBC,(4分)
∵EB=EF,
∴∠EBC=∠EFC;(5分)
∴∠EDC=∠EFC;(6分)
∵∠DGE=∠FGC,
∴△DGE∽△FGC;(7分)
∴
| EG |
| CG |
| GD |
| FG |
(2)解:∠ADC=2∠FDC.(9分)
证明如下:∵
| EG |
| CG |
| GD |
| FG |
∴△CGE∽△FGD;(10分)
∵EF⊥CD,DA=DC,
∴∠DAC=∠DCA=∠DFG=90°-∠FDC,(11分)
∴∠ADC=180°-2∠DAC=180°-2(90°-∠FDC)=2∠FDC.(12分)
点评:本题主要考查全等三角形的判定及性质、相似三角形的判定及性质、菱形的性质等知识点,属于综合题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 (2012•重庆)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(2012•重庆)已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2. 已知:如图,在菱形ABCD中,E为BC边上一点,∠AED=∠B.
已知:如图,在菱形ABCD中,E为BC边上一点,∠AED=∠B. (2013•贵阳)已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(2013•贵阳)已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC. 已知,如图,在菱形ABCD中,AE⊥BC于点E,BE=12,sinD=
已知,如图,在菱形ABCD中,AE⊥BC于点E,BE=12,sinD=