摘要：[解析]根据题目中存在的等量关系.容易填写出未知的量.然后建立w与x之间的函数关系式. [答案]解:(1)填表 依题意得:. 解得: . (2) w与x之间的函数关系为:. 依题意得:.∴40≤≤240 在中.∵2>0.∴随的增大而增大. 故当＝40时.总运费最小. 此时调运方案为如下表. (3)由题意知 ∴0<<2时.(2)中调运方案总运费最小, =2时.在40≤≤240的前提下调运.方案的总运费不变, 2<<15时.＝240总运费最小. 其调运方案如下表
网址：http://m.1010jiajiao.com/timu3_id_478853[举报]
某工厂拟建一座平面图形为矩形且面积为200m2的三级污水处理池（平面图如图），由于地形限制，三级污水处理池的长、宽都不能超过16米，如果池的外围墙建造单价为每米400元，中间两条隔墙建造单价为每米300元，池底建造单价为每平方米80元（池墙厚度忽略不计）。
（1）当三级污水处理池总造价为47200元时，求池长x；
（2）如果规定总造价越低就越合算，那么根据题目中提供的信息以47200元为总造价来修建三级污水处理池是否最合算？请说明理由。
查看习题详情和答案>>
（2）如果规定总造价越低就越合算，那么根据题目中提供的信息以47200元为总造价来修建三级污水处理池是否最合算？请说明理由。
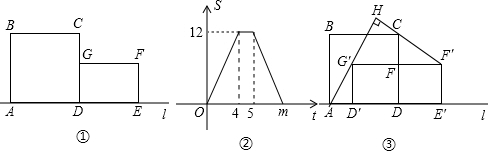
已知：如图①，正方形ABCD与矩形DEFG的边AD、DE在同一直线l上，点G在CD上．正方形ABCD的边长为a，矩形DEFG的长DE为b，宽DG为3（其中a＞b＞3）．若矩形DEFG沿直线l向左以每秒1个单位的长度的速度运动（点D、E始终在直线l上）．若矩形DEFG在运动过程中与正方形ABCD的重叠部分的面积记作S，运动时间记为t秒（0≤t≤m），其中S与t的函数图象如图②所示．矩形DEFG的顶点经运动后的对应点分别记作D′、E′、F′、G′．
（1）根据题目所提供的信息，可求得b= ，a= ，m= ；
（2）连接AG′、CF′，设以AG′和CF′为边的两个正方形的面积之和为y，求当0≤t≤5时，y与时间t之间的函数关系式，并求出y的最小值以及y取最小值时t的值；
（3）如图③，这是在矩形DEFG运动过程中，直线AG′第一次与直线CF′垂直的情形，求此时t的值．并探究：在矩形DEFG继续运动的过程中，直线AG′与直线CF′是否存在平行或再次垂直的情形？如果存在，请画出图形，并求出t的值；否则，请说明理由．
查看习题详情和答案>>
（1）根据题目所提供的信息，可求得b=
（2）连接AG′、CF′，设以AG′和CF′为边的两个正方形的面积之和为y，求当0≤t≤5时，y与时间t之间的函数关系式，并求出y的最小值以及y取最小值时t的值；
（3）如图③，这是在矩形DEFG运动过程中，直线AG′第一次与直线CF′垂直的情形，求此时t的值．并探究：在矩形DEFG继续运动的过程中，直线AG′与直线CF′是否存在平行或再次垂直的情形？如果存在，请画出图形，并求出t的值；否则，请说明理由．
查看习题详情和答案>>
（2012•南京）下框中是小明对一道题目的解答以及老师的批改．
题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留3m的空地，其他三侧内墙各保留1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是288m2？ 解：设矩形蔬菜种植区域的宽为xm，则长为2xm，  根据题意，得x•2x=288． 解这个方程，得x1=-12（不合题意，舍去），x2=12 所以温室的长为2×12+3+1=28（m），宽为12+1+1=14（m） 答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288m2．我的结果也正确！ 小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个？． 结果为何正确呢？  （1）请指出小明解答中存在的问题，并补充缺少的过程： 变化一下会怎样… （2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB=2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由． 查看习题详情和答案>> |
积为4，试说明理由．”题目中有一段被墨水污染了的无法辨认的文字．