摘要：如图.以矩形OABC的顶点O为原点.OA所在的直线为x轴.OC所在的直线为y轴.建立平面直角坐标系．已知OA＝3.OC＝2.点E是AB的中点.在OA上取一点D.将△BDA沿BD翻折.使点A落在BC边上的点F处． (1)直接写出点E.F的坐标, (2)设顶点为F的抛物线交y轴正半轴于点P.且以点E.F.P为顶点的三角形是等腰三角形.求该抛物线的解析式, (3)在x轴.y轴上是否分别存在点M.N.使得四边形MNFE的周长最小?如果存在.求出周长的最小值,如果不存在.请说明理由． 第8课时 分类讨论题 答案
网址：http://m.1010jiajiao.com/timu3_id_478800[举报]
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点．在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．直接写出点E的坐标（3，1）
（3，1）
，F坐标是（1，2）
（1，2）
．
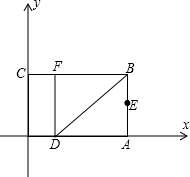如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．（1）直接写出点E、F的坐标；
（2）若P在坐标轴上，且以点E、F、C、P为顶点的四边形是梯形，求点P的坐标；
（3）在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．（Ⅰ）直接写出点E、F的坐标；
（Ⅱ）若M为x轴上的动点，N为y轴上的动点，当四边形MNFE的周长最小时，求出点M、N的坐标，并求出周长的最小值． 查看习题详情和答案>>
10、如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系、已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处，若在y轴上存在点P，且满足FE=FP，则P点坐标为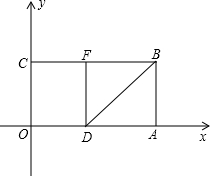
如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在直线为y轴，建立平面直角坐标系，已知OA=3，OC=2．在OA上取一点D，将△BDA沿BD对折，使点A落在BC边上的点F处．