摘要：如图.在直角坐标系中.O是原点.A.B.C三点的坐标分别为A.四边形OABC是梯形.点P.Q同时从原点出发.分别作匀速运动.其中点P沿OA向终点A运动.速度为每秒1个单位.点Q沿OC.CB向终点B运动.当这两点有一点到达自己的终点时.另一点也停止运动. ⑴ 求出直线OC的解析式及经过O.A.C三点的抛物线的解析式. ⑵ 试在⑴中的抛物线上找一点D.使得以O.A.D为顶点的三角形与△AOC全等.请直接写出点D的坐标. ⑶ 设从出发起.运动了t秒.如果点Q的速度为每秒2个单位.试写出点Q的坐标.并写出此时t的取值范围. ⑷ 设从出发起.运动了t秒.当P.Q两点运动的路程之和恰好等于梯形OABC的周长的一半.这时.直线PQ能否把梯形的面积也分成相等的两部分.如有可能.请求出t的值,如不可能.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_478686[举报]
如图，在直角坐标系中，以原点为圆心，半径为5的圆内有一点P（0，-3），则经过点P的所有弦中最短的弦长为
27、如图，在直角坐标系中，设一动点M自P0（1，0）处向上运动1个单位至P1（1，1），然后向左运动2个单位至P2处，再向下运动3个单位至P3处，再向右运动4个单位至P4处，再向上运动5个单位至P5处，…如此继续运动下去，设Pn（xn，yn），n=1，2，3，…则x1+x2+…+x99+x100=50
．
如图，在直角坐标系中，O为坐标原点，矩形ABCD的边AD与x轴的正半轴重合，另三边都在第四象限内，已知点A（1，0），AB=2，AD=3，点E为OD的中点，以AD为直径作⊙M，经过A、D两点的抛物线y=ax2+bx+c的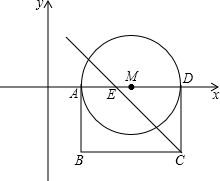
顶点为P．
（1）求经过C、E两点的直线的解析式；
（2）如果点P同时在⊙M和矩形ABCD内部，求a的取值范围；
（3）过点B作⊙M的切线交边CD于F点，当PF∥AD时，判断直线CE与y轴的交点是否在抛物线上，并说明理由． 查看习题详情和答案>>
顶点为P．（1）求经过C、E两点的直线的解析式；
（2）如果点P同时在⊙M和矩形ABCD内部，求a的取值范围；
（3）过点B作⊙M的切线交边CD于F点，当PF∥AD时，判断直线CE与y轴的交点是否在抛物线上，并说明理由． 查看习题详情和答案>>
y=
已如：如图，在直角坐标系中，以y轴上的点C为圆心，2为半径的圆与x轴相切于原点O，AB为⊙C的直径，PA切⊙O于点A，交x轴的负半轴于点P，连接PC交OA于点D．