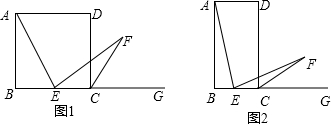
摘要：如图1.四边形ABCD是正方形.G是CD边上的一个动点(点G与C.D不重合).以CG为一边在正方形ABCD外作正方形CEFG.连结BG.DE．我们探究下列图中线段BG.线段DE的长度关系及所在直线的位置关系: (1)①猜想如图1中线段BG.线段DE的长度关系及所在直线的位置关系, ②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度.得到如图2.如图3情形．请你通过观察.测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断． (2)将原题中正方形改为矩形.且AB=a.BC=b.CE=ka. CG=kb (ab.k0).第(1)题①中得到的结论哪些成立.哪些不成立?若成立.以图5为例简要说明理由．
网址：http://m.1010jiajiao.com/timu3_id_477570[举报]
如图1，四边形ABCD是矩形，AB=3CB，G是CD边上的一点，且CG=BC．
（1）以CG为一边在矩形ABCD右侧作矩形CEFG，使矩形ABCD≌矩形CEFG；（要求尺规作图，不写作法）
（2）连接BG，DE．试问图中线段BG、线段DE的长度关系及所在直线的位置关系，并说明理由；
（3）将图1中的矩形CEFG绕着点C按逆时针方向旋转任意角度α，得到如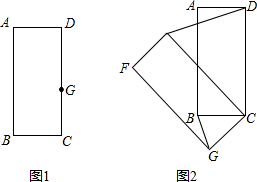
图2，请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并证明你的判断．
查看习题详情和答案>>
（1）以CG为一边在矩形ABCD右侧作矩形CEFG，使矩形ABCD≌矩形CEFG；（要求尺规作图，不写作法）
（2）连接BG，DE．试问图中线段BG、线段DE的长度关系及所在直线的位置关系，并说明理由；
（3）将图1中的矩形CEFG绕着点C按逆时针方向旋转任意角度α，得到如
图2，请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并证明你的判断．
查看习题详情和答案>>
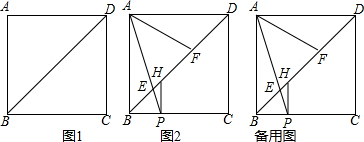
如图1，四边形ABCD是由两个全等的等腰直角三角形斜边重合在一起组成的平面图形．如图2，点P是边BC上一点，PH⊥BC交BD于点H，连接AP交BD于点E，点F为DH中点，连接AF．
（1）求证：四边形ABCD为正方形；
（2）当点P在线段BC上运动时，∠PAF的大小是否会发生变化？若不变，请求出∠PAF的值；若变化，请说明理由；
（3）求证：BE2+DF2=EF2．
查看习题详情和答案>>
（1）求证：四边形ABCD为正方形；
（2）当点P在线段BC上运动时，∠PAF的大小是否会发生变化？若不变，请求出∠PAF的值；若变化，请说明理由；
（3）求证：BE2+DF2=EF2．
（2013•浙江一模）阅读并解答下列问题：
问题一．如图1，在?ABCD中，AD=20，AB=30，∠A=60°，点P是线段AD上的动点，连PB，当AP=
问题二．如图2，四边形ABCD是边长为20的菱形，且∠DAB=60°，P是线段AC上的动点，E在AB上，且AE=
AB，连PE，PB，问当AP长为多少时，PE+PB的值最小，并求这个最小值．
问题三．如图3，在矩形ABCD中，AB=20，CB=10，P，Q分别是线段AC，AB上的动点，问当AP长为多少时，PQ+PB的值最小，并求这个最小值．
查看习题详情和答案>>
问题一．如图1，在?ABCD中，AD=20，AB=30，∠A=60°，点P是线段AD上的动点，连PB，当AP=
15
15
时，PB最小值为15
| 3 |
15
．| 3 |
问题二．如图2，四边形ABCD是边长为20的菱形，且∠DAB=60°，P是线段AC上的动点，E在AB上，且AE=
| 1 |
| 4 |
问题三．如图3，在矩形ABCD中，AB=20，CB=10，P，Q分别是线段AC，AB上的动点，问当AP长为多少时，PQ+PB的值最小，并求这个最小值．
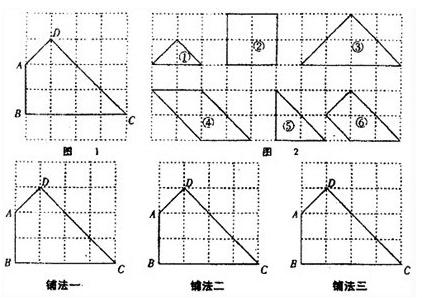22、如图1，四边形ABCD是一位师傅用地板砖铺设地板尚未完工的地板图形，为了节省材料，他准备在剩余的六块砖中如图2所示①②③④⑤⑥、挑选若干块进行铺设，请你在下列网格纸上帮他设计3种不同的铺法示意图．在图上画出分割线，标上地砖序号即可．