题目内容
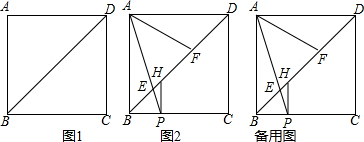
如图1,四边形ABCD是由两个全等的等腰直角三角形斜边重合在一起组成的平面图形.如图2,点P是边BC上一点,PH⊥BC交BD于点H,连接AP交BD于点E,点F为DH中点,连接AF.
(1)求证:四边形ABCD为正方形;
(2)当点P在线段BC上运动时,∠PAF的大小是否会发生变化?若不变,请求出∠PAF的值;若变化,请说明理由;
(3)求证:BE2+DF2=EF2.
(1)求证:四边形ABCD为正方形;
(2)当点P在线段BC上运动时,∠PAF的大小是否会发生变化?若不变,请求出∠PAF的值;若变化,请说明理由;
(3)求证:BE2+DF2=EF2.

分析:(1)根据等腰直角三角形性质得出AD=AB=DC=BC,∠A=90°,根据正方形的判定推出即可.
(2)连接PF,并延长PF交CD的延长线于M,连接AM,证△FHP≌△FDM,推出PF=MF,PH=DM,求出BP=PH=DM,证△ABP≌△ADM,推出AP=AM,∠BAP=∠MAD,得出△PAM是等腰直角三角形,根据等腰直角三角形推出即可.
(3)在AM上截取AN=AE,连接NF,证△BAE≌△DAN,推出BE=DN,∠ABE=∠ADN=45°=∠ADF,求出∠NDF=90°,在Rt△DNF中,由勾股定理求出ND2+DF2=NF2,证△NAF≌△EAF,推出EF=FN,即可得出答案.
(2)连接PF,并延长PF交CD的延长线于M,连接AM,证△FHP≌△FDM,推出PF=MF,PH=DM,求出BP=PH=DM,证△ABP≌△ADM,推出AP=AM,∠BAP=∠MAD,得出△PAM是等腰直角三角形,根据等腰直角三角形推出即可.
(3)在AM上截取AN=AE,连接NF,证△BAE≌△DAN,推出BE=DN,∠ABE=∠ADN=45°=∠ADF,求出∠NDF=90°,在Rt△DNF中,由勾股定理求出ND2+DF2=NF2,证△NAF≌△EAF,推出EF=FN,即可得出答案.
解答:(1)证明:∵四边形ABCD是由两个全等的等腰直角三角形斜边重合在一起组成的平面图形,
∴AD=AB=DC=BC,∠A=90°,
∴四边形ABCD是正方形;
(2)解:不变化,
理由是:连接PF,并延长PF交CD的延长线于M,连接AM,如图2,
∵∠C=90°,PH⊥BC,
∴∠C=∠HPB=90°,
∴PH∥CD,
∴∠PHF=∠MDF,
∵F为DH中点,
∴HF=DF,
在△FHP和△FDM中
∴△FHP≌△FDM,
∴PF=MF,PH=DM,
∵PH⊥BC,
∴∠HPB=90°,
∵BC=CD,∠C=90°,
∴∠HBP=45°,
∴∠BHP=45°=∠HBP,
∴BP=PH,
∴DM=BP,
∵四边形ABCD是正方形,
∴AB=AD,∠ABP=∠ADM=90°,
在△ABP和△ADM中
∴△ABP≌△ADM(SAS),
∴AP=AM,∠BAP=∠MAD,
∵∠DAB=90°,
∴∠MAP=∠MAD+∠DAP=∠BAP+∠DAP=∠DAB=90°,
∴△PAM是等腰直角三角形,
∵PF=MF,
∴∠EAF=∠MAF=
∠MAP=45°,
即当点P在线段BC上运动时,∠PAF的大小不会发生变化,∠PAF的值永远是45°;
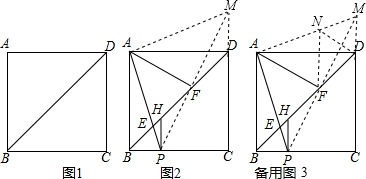
(3)证明:在AM上截取AN=AE,连接NF,如图3,
∵△ABD是等腰直角三角形,
∴∠ABD=∠ADB=45°,
∵在△BAE和△DAN中
∴△BAE≌△DAN(SAS),
∴BE=DN,∠ABE=∠ADN=45°=∠ADF,
∴∠NDF=45°+45°=90°,
在Rt△DNF中,由勾股定理得:ND2+DF2=NF2,
∵∠BAD=90°,∠EAF=45°,
∴∠NAF=∠NAD+∠DAF=∠BAE+∠DAF=90°-45°=45°,
∴∠NAF=∠EAF=45°,
在△NAF和△EAF中
∴△NAF≌△EAF(SAS),
∴EF=FN,
∵ND2+DF2=NF2,DN=BE,
∴BE2+DF2=EF2.
∴AD=AB=DC=BC,∠A=90°,
∴四边形ABCD是正方形;
(2)解:不变化,
理由是:连接PF,并延长PF交CD的延长线于M,连接AM,如图2,
∵∠C=90°,PH⊥BC,
∴∠C=∠HPB=90°,
∴PH∥CD,
∴∠PHF=∠MDF,
∵F为DH中点,
∴HF=DF,
在△FHP和△FDM中
|
∴△FHP≌△FDM,
∴PF=MF,PH=DM,
∵PH⊥BC,
∴∠HPB=90°,
∵BC=CD,∠C=90°,
∴∠HBP=45°,
∴∠BHP=45°=∠HBP,
∴BP=PH,
∴DM=BP,
∵四边形ABCD是正方形,
∴AB=AD,∠ABP=∠ADM=90°,
在△ABP和△ADM中
|
∴△ABP≌△ADM(SAS),
∴AP=AM,∠BAP=∠MAD,
∵∠DAB=90°,
∴∠MAP=∠MAD+∠DAP=∠BAP+∠DAP=∠DAB=90°,
∴△PAM是等腰直角三角形,
∵PF=MF,
∴∠EAF=∠MAF=
| 1 |
| 2 |
即当点P在线段BC上运动时,∠PAF的大小不会发生变化,∠PAF的值永远是45°;

(3)证明:在AM上截取AN=AE,连接NF,如图3,
∵△ABD是等腰直角三角形,
∴∠ABD=∠ADB=45°,
∵在△BAE和△DAN中
|
∴△BAE≌△DAN(SAS),
∴BE=DN,∠ABE=∠ADN=45°=∠ADF,
∴∠NDF=45°+45°=90°,
在Rt△DNF中,由勾股定理得:ND2+DF2=NF2,
∵∠BAD=90°,∠EAF=45°,
∴∠NAF=∠NAD+∠DAF=∠BAE+∠DAF=90°-45°=45°,
∴∠NAF=∠EAF=45°,
在△NAF和△EAF中
|
∴△NAF≌△EAF(SAS),
∴EF=FN,
∵ND2+DF2=NF2,DN=BE,
∴BE2+DF2=EF2.
点评:本题考查了等腰直角三角形性质,正方形性质和判定,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力,有一定的难度.

练习册系列答案
相关题目
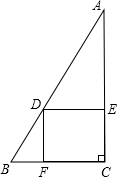 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.