题目内容
（2013•浙江一模）阅读并解答下列问题：
问题一．如图1，在?ABCD中，AD=20，AB=30，∠A=60°，点P是线段AD上的动点，连PB，当AP=
问题二．如图2，四边形ABCD是边长为20的菱形，且∠DAB=60°，P是线段AC上的动点，E在AB上，且AE=
AB，连PE，PB，问当AP长为多少时，PE+PB的值最小，并求这个最小值．
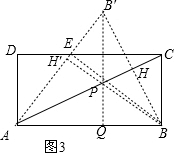
问题三．如图3，在矩形ABCD中，AB=20，CB=10，P，Q分别是线段AC，AB上的动点，问当AP长为多少时，PQ+PB的值最小，并求这个最小值．
问题一．如图1，在?ABCD中，AD=20，AB=30，∠A=60°，点P是线段AD上的动点，连PB，当AP=
15
15
时，PB最小值为15
| 3 |
15
．| 3 |
问题二．如图2，四边形ABCD是边长为20的菱形，且∠DAB=60°，P是线段AC上的动点，E在AB上，且AE=
| 1 |
| 4 |
问题三．如图3，在矩形ABCD中，AB=20，CB=10，P，Q分别是线段AC，AB上的动点，问当AP长为多少时，PQ+PB的值最小，并求这个最小值．
分析：（1）如图1，过点B作BP⊥AD于P，根据直角三角形的性质和勾股定理就可以求出结论；
（2）如图2，连接BD、ED交AC于点P，作DF⊥AB于F．由菱形的性质可以得出AC的值，再由△APE∽△CPD就根据相似三角形的性质就可以得出结论；
（3）作B关于AC的对称点B′，连结AB′，则N点关于AC的对称点N′在AB′上，这时，B到M到N的最小值等于B→M→N′的最小值，等于B到AB′的距离BH′，连结B与AB′和DC的交点P，再由三角形的面积公式可求出S△ABP的值，根据对称的性质可知∠PAC=∠BAC=∠PCA，利用勾股定理可求出PA的值，再由S△ABP=
PA•BH′即可求解．
（2）如图2，连接BD、ED交AC于点P，作DF⊥AB于F．由菱形的性质可以得出AC的值，再由△APE∽△CPD就根据相似三角形的性质就可以得出结论；
（3）作B关于AC的对称点B′，连结AB′，则N点关于AC的对称点N′在AB′上，这时，B到M到N的最小值等于B→M→N′的最小值，等于B到AB′的距离BH′，连结B与AB′和DC的交点P，再由三角形的面积公式可求出S△ABP的值，根据对称的性质可知∠PAC=∠BAC=∠PCA，利用勾股定理可求出PA的值，再由S△ABP=
| 1 |
| 2 |
解答：解：（1）如图1，过点B作BP⊥AD于P，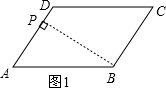
∴∠APB=90°．
∵∠A=60°，
∴∠ABP=30°，
∴AP=
AB．
∵AB=30，
∴AP=15．
在Rt△ABP中，由勾股定理，得
BP=
=15
．
（2）如图2，连结BD，连结DE交AC于点P，作DF⊥AB于F．
∵四边形ABCD是菱形，
∴AB=BC=CD=DA，AB∥CD．AC⊥BD，DO=BO=
DB，AO=CO=
AC，∠OAB=
∠DAB．
∵∠DAB=60°，
∴△ABD和△CDB是等边三角形，
∴AF=
AB=10，．
在Rt△ADF中，由勾股定理，得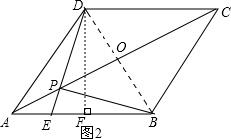
DF=10
．
∵AE=
AB，且AB=20，
∴AE=5．
∴EF=5．
在Rt△EFD中，由勾股定理，得
DE=
=5
，
∴BP+PE的最小值为5
．
在Rt△ABO中，由勾股定理，得
AO=10
．
∴AC=20
∴△AEP∽△CDP，
∴
=
．
∴
=
，
∴AP=4
．
答：当AP长为4
时，PE+PB的值最小为5
；
（3）如图3，作B关于AC的对称点B′，作B′Q⊥QB于Q，交AC于P．
连结AB′，则Q点关于AC的对称点H′在AB′上，
∴∠AHB=∠AHB′=90°，BH=B′H，
∴AB′=AB，
∴∠AB′H=∠ABH．
这时，B到P到Q的最小值等于B→P→H′的最小值，
等于B到AB′的距离BH′，
连结AB′和DC的交点E，
则S△ABE=
×20×10=100，
由对称知识，∠EAC=∠BAC=∠ECA，
所以EA=EC，令EA=x，则EC=x，ED=20-x，
在Rt△ADE中，EA2=ED2+AD2，
所以x2=（20-x）2+102，
所以x=12.5，
因为S△ABE=
EA•BH′，
所以BH′=
=
=16．
在△BB′H′和△B′BQ中，
，
∴△BB′H′≌△B′BQ（SAS），
∴BH′=B′Q=10．
在Rt△ABC中，由勾股定理，得
AC=10
．
∵S△ABC=
=
，
∴
=
，
∴BH=4
，
∴BB′=8
．
在Rt△BB′Q中，由勾股定理，得
QB=8，
∴AQ=12．
∵PQ⊥AB，
∴∠AQP=90°，且∠ABC=90°，
∴PQ∥BC．
∴△AQP∽△ABC，
∴
=
，
∴
=
，
∴AP=6
．
答：AP长为6
时，PQ+PB的值最小为16．
故答案为：15，15
．
∴∠APB=90°．
∵∠A=60°，
∴∠ABP=30°，
∴AP=
| 1 |
| 2 |
∵AB=30，
∴AP=15．
在Rt△ABP中，由勾股定理，得
BP=
| 302-152 |
| 3 |
（2）如图2，连结BD，连结DE交AC于点P，作DF⊥AB于F．
∵四边形ABCD是菱形，
∴AB=BC=CD=DA，AB∥CD．AC⊥BD，DO=BO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DAB=60°，
∴△ABD和△CDB是等边三角形，
∴AF=
| 1 |
| 2 |
在Rt△ADF中，由勾股定理，得
DF=10
| 3 |
∵AE=
| 1 |
| 4 |
∴AE=5．
∴EF=5．
在Rt△EFD中，由勾股定理，得
DE=
| 300+25 |
| 13 |
∴BP+PE的最小值为5
| 13 |
在Rt△ABO中，由勾股定理，得
AO=10
| 3 |
∴AC=20
| 3 |
∴△AEP∽△CDP，
∴
| AE |
| DC |
| AP |
| PC |
∴
| 5 |
| 20 |
| AP | ||
20
|
∴AP=4
| 3 |
答：当AP长为4
| 3 |
| 13 |
（3）如图3，作B关于AC的对称点B′，作B′Q⊥QB于Q，交AC于P．
连结AB′，则Q点关于AC的对称点H′在AB′上，
∴∠AHB=∠AHB′=90°，BH=B′H，
∴AB′=AB，
∴∠AB′H=∠ABH．
这时，B到P到Q的最小值等于B→P→H′的最小值，
等于B到AB′的距离BH′，
连结AB′和DC的交点E，
则S△ABE=
| 1 |
| 2 |
由对称知识，∠EAC=∠BAC=∠ECA，
所以EA=EC，令EA=x，则EC=x，ED=20-x，
在Rt△ADE中，EA2=ED2+AD2，
所以x2=（20-x）2+102，
所以x=12.5，
因为S△ABE=
| 1 |
| 2 |
所以BH′=
| 2S△ABE |
| EA |
| 100×2 |
| 12.5 |
在△BB′H′和△B′BQ中，
|
∴△BB′H′≌△B′BQ（SAS），
∴BH′=B′Q=10．
在Rt△ABC中，由勾股定理，得
AC=10
| 5 |
∵S△ABC=
| AB•BC |
| 2 |
| AC•BH |
| 2 |
∴
| 20×10 |
| 2 |
10
| ||
| 2 |
∴BH=4
| 5 |
∴BB′=8
| 5 |
在Rt△BB′Q中，由勾股定理，得
QB=8，
∴AQ=12．
∵PQ⊥AB，
∴∠AQP=90°，且∠ABC=90°，
∴PQ∥BC．
∴△AQP∽△ABC，
∴
| AP |
| AC |
| AQ |
| AB |
∴
| AP | ||
10
|
| 12 |
| 20 |
∴AP=6
| 5 |
答：AP长为6
| 5 |
故答案为：15，15
| 3 |
点评：本题考查的是最短路线问题，考查轴对称的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，相似三角形的判定及性质的运用，等边三角形的性质的运用，解答第三问时作出B点关于直线AC对称的点B′是解答此题的关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
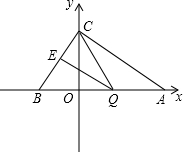（2013•浙江一模）如图，已知在平面直角坐标系中，点A（4，0）、B（-3，0），点C在y轴正半轴上，且tan∠CAO=1，点Q是线段AB上的动点，过点Q作QE∥AC交BC于点E．
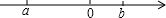（2013•浙江一模）实数在数轴上的位置如图所示，下列式子正确的是（ ）