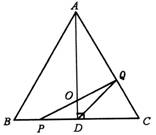
摘要：如图.在△ABC中.已知AB = BC = AC = 4 .AD⊥BC于D.P.Q分别从B.C两点同时出发.其中P点沿BC向终点C运动.速度为1／.点Q沿CA.AB向终点B运动.速度为2／.设它们的运动时间为 ⑴求为何值时.PQ⊥AC, ⑵设△PQD的面积为.当时.求与之间的函数关系式, ⑶当时.试探究△POD与△QOD的面积关系. 附答案
网址：http://m.1010jiajiao.com/timu3_id_474512[举报]
如图，在△ABC中，已知AB=BC=AC=4cm，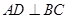
于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s，点Q沿CA，AB向终点B运动，速度为2cm/s，设它们运动的时间为t(s)，
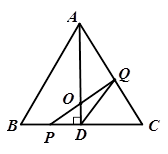
（1）求t为何值时，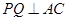
；
（2）当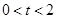
时，求证：AD平分△PQD的面积；
（3）当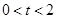时，求△PQD面积的最大值.
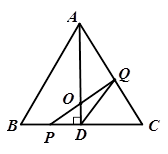
于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s，点Q沿CA，AB向终点B运动，速度为2cm/s，设它们运动的时间为t(s)，（1）求t为何值时，
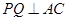；（2）当
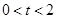时，求证：AD平分△PQD的面积；（3）当
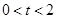时，求△PQD面积的最大值.
是高线， BC＝8cm， 则BD的长等于（ ）
B.8cm C.5cm D.4cm 
如图，在△ABC中，已知AB=BC=CA=4cm，AD⊥BC于D．点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点Q沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x（s）．（1）当x=
（2）设△PQD的面积为y（cm2），当0＜x＜2时，求y与x的函数关系式为
（3）当0＜x＜2时，求证：AD平分△PQD的面积；
（4）探索以PQ为直径的圆与AC的位置关系，请写出相应位置关系的x的取值范围（不要求写出过程）． 查看习题详情和答案>>
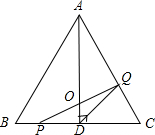运动，速度为1cm/s，Q沿CA、AB向终点B运动，速度为2cm/s，设它们的运动时间为x（s）．