摘要：23． 已知等边三角形纸片的边长为.为边上的点.过点作交于点．于点.过点作于点.把三角形纸片分别沿按图1所示方式折叠.点分别落在点..处．若点..在矩形内或其边上.且互不重合.此时我们称为“重叠三角形 ． (1)若把三角形纸片放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形).点恰好落在网格图中的格点上．如图2所示.请直接写出此时重叠三角形的面积, (2)实验探究:设的长为.若重叠三角形存在．试用含的代数式表示重叠三角形的面积.并写出的取值范围(直接写出结果.备用图供实验.探究使用)． 解:(1)重叠三角形的面积为 , (2)用含的代数式表示重叠三角形的面积为 ,的取值范围为 ．
网址：http://m.1010jiajiao.com/timu3_id_473419[举报]
已知等边三角形纸片
的边长为
，
为
边上的点，过点作
交
于点
．
于点
，过点作
于点
，把三角形纸片分别沿
按图1所示方式折叠，点
分别落在点
，
，
处．若点，，在矩形
内或其边上，且互不重合，此时我们称
（即图中阴影部分）为“重叠三角形”．
（1）若把三角形纸片放在等边三角形网格中（图中每个小三角形都是边长为1的等边三角形），点
恰好落在网格图中的格点上．如图2所示，请直接写出此时重叠三角形
的面积；
（2）实验探究：设
的长为
，若重叠三角形存在．试用含的代数式表示重叠三角形的面积，并写出的取值范围（直接写出结果，备用图供实验，探究使用）．
23、观察探索题：如图，已知三角形ABC，延长BC到D，过点C作CE∥AB．由于AB∥CE，所以可得到∠B=∠3和∠A=∠2．又因为∠1+∠2+∠3组成一个平角为180°，通过等量代换可以得到三角形ABC的三个内角的和为180°，即∠A+∠B+∠ACB=180°．
试根据以上叙述，写出已知、求证及说明∠A+∠B+∠ACB=180°的过程．
已知：延长三角形ABC的边BC到D，过C作CE∥AB．
求证：∠A+∠B+∠ACB=180°
证明：
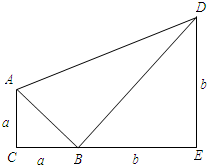
如图，已知等腰直角三角形ACB的边AC=BC=a，等腰直角三角形BED的边BE=DE=b，且a＜b，点C、B、E放置在一条直线上，连接AD．（1）求三角形ABD的面积．
（2）如果点P是线段CE的中点，连接AP、DP得到三角形APD，求三角形APD的面积．
（3）（2）中的三角形APD与三角形ABD面积哪个较大？大多少？（结果都可用a、b代数式表示，并化简．）
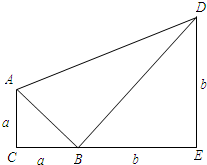如图，已知等腰直角三角形ACB的边AC=BC=a，等腰直角三角形BED的边BE=DE=b，且a＜b，点C、B、E放置在一条直线上，连接AD．