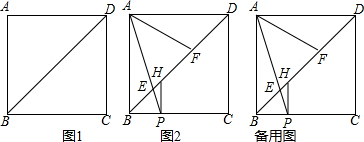
摘要：28．两个全等的等腰直角三角形和三角形如图1放置.点在同一条直线上．那么点C.A.E在同一条直线上, ①在图1中.作的平分线.过点作.垂足为, ②猜想:线段的关系.结论是: . 中的“等腰直角三角形 换成“直角三角形 .其它条件不变.如图2, 连结CE.请问你猜想的BF与CE的关系是否仍然成立?若成立.请证明,若不成立.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_472308[举报]
如图，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若△ABC固定不动，△AFG绕点A旋转，AF、AG与边BC的交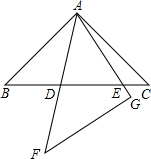
点分别为D、E（点D不与点B重合，点E不与点C重合），设BE=m，CD=n．
（1）△ABE与△DCA是否相似？请加以说明．
（2）求m与n的函数关系式，直接写出自变量n的取值范围．
（3）当BE=CD时，分别求出线段BD、CE、DE的长，并通过计算验证BD2+CE2=DE2．
（4）在旋转过程中，（3）中的等量关系BD2+CE2=DE2是否始终成立，若成立，请证明；若不成立，请说明理由．
查看习题详情和答案>>
点分别为D、E（点D不与点B重合，点E不与点C重合），设BE=m，CD=n．（1）△ABE与△DCA是否相似？请加以说明．
（2）求m与n的函数关系式，直接写出自变量n的取值范围．
（3）当BE=CD时，分别求出线段BD、CE、DE的长，并通过计算验证BD2+CE2=DE2．
（4）在旋转过程中，（3）中的等量关系BD2+CE2=DE2是否始终成立，若成立，请证明；若不成立，请说明理由．
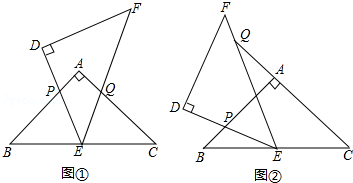
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；若旋转到DE⊥AB时，当BP=a，CQ=
a时，求PQ（用含a的代数式表示）．
查看习题详情和答案>>
如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；若旋转到DE⊥AB时，当BP=a，CQ=
| 9 | 2 |
把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点逆时针旋转（旋转角α满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图②）．（1）在上述旋转过程中，BH与CK有怎样的数量关系四边形CHGK的面积有何变化？证明你发现的结论；
（2）连接HK，在上述旋转过程中，设BH=x，△GKH的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；
（3）在（2）的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的
| 5 | 16 |
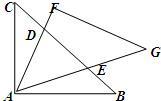13、如图，△ABC与△FAG是两个全等的等腰直角三角形，∠BAC=∠F=90°，BC分别与AF、AG相交于点D、E．则图中不全等的相似三角形有