摘要： 如图.点A(m.m+1).B(m+3.m-1)都在反比例函数的图象上． (1)求m.k的值, (2)如果M为x轴上一点.N为y轴上一点. 以点A.B.M.N为顶点的四边形是平行四边形. 试求直线MN的函数表达式．
网址：http://m.1010jiajiao.com/timu3_id_470923[举报]
（本题满分10分）如图：是7×7的正方形网格，请在所给网格中按下列要求操作：
小题1:（1）请在网格中建立平面直角坐标系，使A点坐标为（－4，2），B点坐标为（－2，4）．
小题2:（2）在第二象限内格点上找一点C，使C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是_________；△ABC周长是____________．（结果保留根号）
小题3:（3）画出三角形ABC以O为位似中心，相似比为
的位似图形．
小题1:（1）请在网格中建立平面直角坐标系，使A点坐标为（－4，2），B点坐标为（－2，4）．
小题2:（2）在第二象限内格点上找一点C，使C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是_________；△ABC周长是____________．（结果保留根号）
小题3:（3）画出三角形ABC以O为位似中心，相似比为
的位似图形．
（本小题满分10分）已知：如图，⊙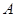
与
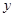轴交于C、D两点，圆心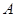的坐标
为（1，0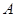），⊙的半径为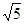
，过点C作⊙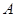的切线交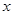
轴于点B（－4，0）
【小题1】（1）求切线BC的解析式；
【小题2】（2）若点P是第一象限内⊙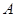上一点，过点P作⊙A的切线与直线BC相交于点G，
且∠CGP＝120°，求点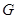
的坐标；
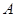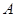【小题3】（3）向左移动⊙（圆心始终保持在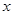轴上），与直线BC交于E、F，在移动过程中是否存在点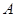，使得△AEF是直角三角形？若存在，求出点 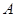的坐标，若不存在，请说明理由．
查看习题详情和答案>>
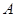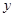与轴交于C、D两点，圆心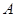的坐标为（1，0），⊙
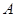的半径为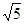，过点C作⊙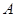的切线交轴于点B（－4，0） |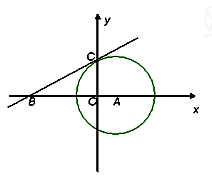
【小题1】（1）求切线BC的解析式；
【小题2】（2）若点P是第一象限内⊙
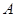上一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP＝120°，求点
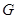的坐标；【小题3】（3）向左移动⊙
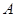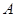（圆心始终保持在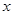轴上），与直线BC交于E、F，在移动过程中是否存在点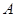，使得△AEF是直角三角形？若存在，求出点 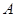的坐标，若不存在，请说明理由．
查看习题详情和答案>>
（本小题满分10分）已知：如图，⊙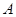
与
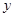轴交于C、D两点，圆心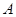的坐标
为（1，0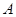），⊙的半径为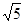
，过点C作⊙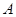的切线交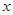
轴于点B（－4，0）
小题1:（1）求切线BC的解析式；
小题2:（2）若点P是第一象限内⊙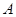上一点，过点P作⊙A的切线与直线BC相交于点G，
且∠CGP＝120°，求点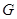
的坐标；
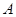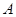小题3:（3）向左移动⊙（圆心始终保持在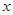轴上），与直线BC交于E、F，在移动过程中是否存在点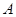，使得△AEF是直角三角形？若存在，求出点 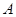的坐标，若不存在，请说明理由．
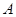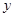与轴交于C、D两点，圆心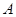的坐标为（1，0），⊙
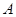的半径为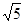，过点C作⊙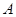的切线交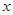轴于点B（－4，0） |
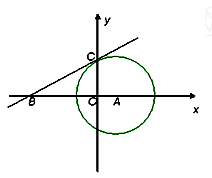小题1:（1）求切线BC的解析式；
小题2:（2）若点P是第一象限内⊙
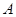上一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP＝120°，求点
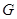的坐标；小题3:（3）向左移动⊙
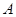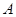（圆心始终保持在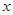轴上），与直线BC交于E、F，在移动过程中是否存在点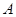，使得△AEF是直角三角形？若存在，求出点 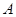的坐标，若不存在，请说明理由．
