题目内容
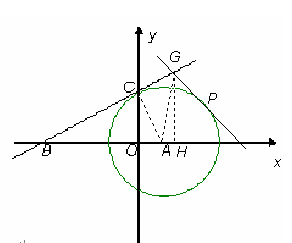
(本小题满分10分)已知:如图,⊙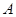 与
与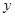 轴交于C、D两点,圆心
轴交于C、D两点,圆心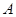 的坐标
的坐标为(1,0),⊙
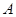 的半径为
的半径为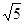 ,过点C作⊙
,过点C作⊙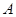 的切线交
的切线交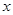 轴于点B(-4,0)
轴于点B(-4,0) |
【小题1】(1)求切线BC的解析式;
【小题2】(2)若点P是第一象限内⊙
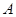 上一点,过点P作⊙A的切线与直线BC相交于点G,
上一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点
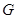 的坐标;
的坐标;【小题3】(3)向左移动⊙
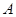 (圆心
(圆心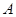 始终保持在
始终保持在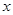 轴上),与直线BC交于E、F,在移动过程中是否存在点
轴上),与直线BC交于E、F,在移动过程中是否存在点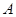 ,使得△AEF是直角三角形?若存在,求出点
,使得△AEF是直角三角形?若存在,求出点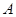 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【小题1】(1)连接
 ,∵
,∵ 是⊙A的切线,∴
是⊙A的切线,∴ .
.∴
 .
.∵
 ,∴
,∴ ,∴
,∴ .
.∴△
 ∽△
∽△ ,∴
,∴ .
.即
 ,∴
,∴ .∴
.∴ 点坐标是(
点坐标是( 0,2).
0,2).设直线
 的解析式为
的解析式为 ,∵该直线经过点B(-4,0)与
,∵该直线经过点B(-4,0)与 点
点
 (0,2),
(0,2),∴
 解得
解得
∴该直线解析式为
 .
.
【小题2】(2)连接
 ,过点
,过点 作
作 .
.由切线长定理知
 .
.在
 中,∵
中,∵ ,
,∴
 .
.在
 中,由勾股定理得
中,由勾股定理得 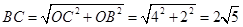 .
.∴
 .
.
又∵
 .
.∴
 ∽
∽ ,∴
,∴ ,
,∴
 .
.则
 是点
是点 的纵坐标,
的纵坐标,∴
 ,解得
,解得 .
.∴点
 的坐标
的坐标 .……………4分
.……………4分【小题3】(3)如图示,当
 在点
在点 的右侧时
的右侧时∵
 、
、 在⊙
在⊙ 上,∴
上,∴ .
.若
 △
△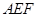 是直角三角形,则
是直角三角形,则 ,且为等腰直角三角形.
,且为等腰直角三角形.过点
 作
作 ,在
,在 中由三角函数可知
中由三角函数可知 .
.又∵
 ∽
∽ ,
,∴
 ,
,∴
 .
.∴
 ,
,∴点
 坐标是
坐标是 .
.当
 在点
在点 的左侧时:同理可求点
的左侧时:同理可求点 坐标是
坐标是 .……………6分
.……………6分 解析:
解析:略

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 .
.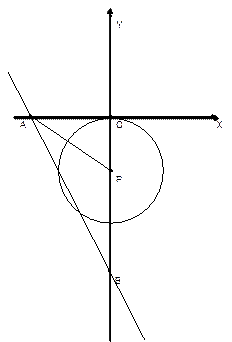
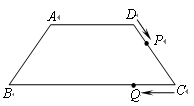

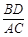 的值.
的值.