摘要: 解:(1)∵MN∥BC.∴∠AMN=∠B.∠ANM=∠C. ∴ △AMN ∽ △ABC. ∴ .即. ∴ AN=x. -----2分 ∴ =.(0<<4) -----3分 (2)如图2.设直线BC与⊙O相切于点D.连结AO.OD.则AO =OD =MN. 在Rt△ABC中.BC ==5. 由(1)知 △AMN ∽ △ABC. ∴ .即. ∴ . ∴ . -------5分 过M点作MQ⊥BC 于Q.则. 在Rt△BMQ与Rt△BCA中.∠B是公共角. ∴ △BMQ∽△BCA. ∴ . ∴ .. ∴ x=. ∴ 当x=时.⊙O与直线BC相切.-------------7分 (3)随点M的运动.当P点落在直线BC上时.连结AP.则O点为AP的中点. ∵ MN∥BC.∴ ∠AMN=∠B.∠AOM=∠APC. ∴ △AMO ∽ △ABP. ∴ . AM=MB=2. 故以下分两种情况讨论: ① 当0<≤2时.. ∴ 当=2时. --------------8分 ② 当2<<4时.设PM.PN分别交BC于E.F. ∵ 四边形AMPN是矩形. ∴ PN∥AM.PN=AM=x. 又∵ MN∥BC. ∴ 四边形MBFN是平行四边形. ∴ FN=BM=4-x. ∴ . 又△PEF ∽ △ACB. ∴ . ∴ . ------------------ 9分 =.--------10分 当2<<4时.. ∴ 当时.满足2<<4.. --------11分 综上所述.当时.值最大.最大值是2. ----------12分
网址:http://m.1010jiajiao.com/timu3_id_465918[举报]
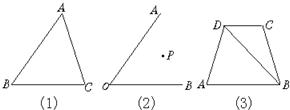
12、用三角尺和直尺画平行线.
(1)过点A画MN∥BC(图(1));
(2)过点P画PE∥OA,交OB于点E;画PH∥OB,交OA于点H(图(2));
(3)过点C画CE∥DA,与AB交于点E;过点C画CF∥DB,与AB的延长线交于点F(图(3)).
查看习题详情和答案>>
(1)过点A画MN∥BC(图(1));
(2)过点P画PE∥OA,交OB于点E;画PH∥OB,交OA于点H(图(2));
(3)过点C画CE∥DA,与AB交于点E;过点C画CF∥DB,与AB的延长线交于点F(图(3)).

(2012•白下区一模)概念理解
把一个或几个图形分割后,不重叠、无缝隙的重新拼成另一个图形的过程叫做“剖分--重拼”.如图1,一个梯形可以剖分--重拼为一个三角形;如图2,任意两个正方形可以剖分--重拼为一个正方形.
尝试操作
如图3,把三角形剖分--重拼为一个矩形.(只要画出示意图,不需说明操作步骤)

阅读解释
如何把一个矩形ABCD(如图4)剖分--重拼为一个正方形呢?操作如下:
①画辅助图.作射线OX,在射线OX上截取OM=AB,MN=BC.以ON为直径作半圆,过点M作MI⊥射线OX,与半圆交于点I;
②图4中,在CD上取点F,使AF=MI,作BE⊥AF,垂足为E.把△ADF沿射线DC平移到△BCH的位置,把△AEB沿射线AF平移到△FGH的位置,得四边形EBHG.
请说明按照上述操作方法得到的四边形EBHG是正方形.

拓展延伸
任意一个多边形是否可以通过若干次的剖分--重拼成一个正方形?如果可以,请简述操作步骤;如果不可以,请说明理由.
查看习题详情和答案>>
把一个或几个图形分割后,不重叠、无缝隙的重新拼成另一个图形的过程叫做“剖分--重拼”.如图1,一个梯形可以剖分--重拼为一个三角形;如图2,任意两个正方形可以剖分--重拼为一个正方形.
尝试操作
如图3,把三角形剖分--重拼为一个矩形.(只要画出示意图,不需说明操作步骤)

阅读解释
如何把一个矩形ABCD(如图4)剖分--重拼为一个正方形呢?操作如下:
①画辅助图.作射线OX,在射线OX上截取OM=AB,MN=BC.以ON为直径作半圆,过点M作MI⊥射线OX,与半圆交于点I;
②图4中,在CD上取点F,使AF=MI,作BE⊥AF,垂足为E.把△ADF沿射线DC平移到△BCH的位置,把△AEB沿射线AF平移到△FGH的位置,得四边形EBHG.
请说明按照上述操作方法得到的四边形EBHG是正方形.

拓展延伸
任意一个多边形是否可以通过若干次的剖分--重拼成一个正方形?如果可以,请简述操作步骤;如果不可以,请说明理由.
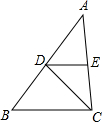 如图,已知CD平分∠ACB,DE∥BC,说明△EDC是等腰三角形的理由.
如图,已知CD平分∠ACB,DE∥BC,说明△EDC是等腰三角形的理由.根据解题的要求,填写适当的内容或理由.
解:∵DE∥BC (已知)
∴
∠EDC=∠DCB
∠EDC=∠DCB
(两直线平行,内错角相等)又
CD平分∠ACB
CD平分∠ACB
(已知) ∴∠ACD=∠BCD (
角平分线的定义
角平分线的定义
)∴∠EDC=∠ACB
∴DE=EC(
等角对等边
等角对等边
)∴△EDC是等腰三角形.
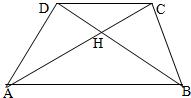 27、梯形ABCD中AB∥CD,对角线AC、BD垂直相交于H,M是AD上的点,MH所在直线交BC于N.在以上前提下,试将下列设定中的两个作为题设,另一个作为结论组成一个正确的命题,并证明这个命题.①AD=BC;②MN⊥BC;③AM=DM.
27、梯形ABCD中AB∥CD,对角线AC、BD垂直相交于H,M是AD上的点,MH所在直线交BC于N.在以上前提下,试将下列设定中的两个作为题设,另一个作为结论组成一个正确的命题,并证明这个命题.①AD=BC;②MN⊥BC;③AM=DM. (2013•南漳县模拟)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
(2013•南漳县模拟)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F