题目内容
(2012•白下区一模)概念理解
把一个或几个图形分割后,不重叠、无缝隙的重新拼成另一个图形的过程叫做“剖分--重拼”.如图1,一个梯形可以剖分--重拼为一个三角形;如图2,任意两个正方形可以剖分--重拼为一个正方形.
尝试操作
如图3,把三角形剖分--重拼为一个矩形.(只要画出示意图,不需说明操作步骤)

阅读解释
如何把一个矩形ABCD(如图4)剖分--重拼为一个正方形呢?操作如下:
①画辅助图.作射线OX,在射线OX上截取OM=AB,MN=BC.以ON为直径作半圆,过点M作MI⊥射线OX,与半圆交于点I;
②图4中,在CD上取点F,使AF=MI,作BE⊥AF,垂足为E.把△ADF沿射线DC平移到△BCH的位置,把△AEB沿射线AF平移到△FGH的位置,得四边形EBHG.
请说明按照上述操作方法得到的四边形EBHG是正方形.

拓展延伸
任意一个多边形是否可以通过若干次的剖分--重拼成一个正方形?如果可以,请简述操作步骤;如果不可以,请说明理由.
把一个或几个图形分割后,不重叠、无缝隙的重新拼成另一个图形的过程叫做“剖分--重拼”.如图1,一个梯形可以剖分--重拼为一个三角形;如图2,任意两个正方形可以剖分--重拼为一个正方形.
尝试操作
如图3,把三角形剖分--重拼为一个矩形.(只要画出示意图,不需说明操作步骤)

阅读解释
如何把一个矩形ABCD(如图4)剖分--重拼为一个正方形呢?操作如下:
①画辅助图.作射线OX,在射线OX上截取OM=AB,MN=BC.以ON为直径作半圆,过点M作MI⊥射线OX,与半圆交于点I;
②图4中,在CD上取点F,使AF=MI,作BE⊥AF,垂足为E.把△ADF沿射线DC平移到△BCH的位置,把△AEB沿射线AF平移到△FGH的位置,得四边形EBHG.
请说明按照上述操作方法得到的四边形EBHG是正方形.

拓展延伸
任意一个多边形是否可以通过若干次的剖分--重拼成一个正方形?如果可以,请简述操作步骤;如果不可以,请说明理由.
分析:尝试操作:先作三角形的一条中位线,把三角形分成一个三角形与梯形,然后作出分成的三角形的高线,分别平移即可;或者先作一条中位线,然后过一个顶点作第三边的高线,把两个三角形平移即可;
阅读解释:连接OI、NI,先利用相似三角形对应边成比例证明IM2=OM•NM,根据操作方法可得AF2=AB•AD,然后证明△DFA和△EAB相似,根据相似三角形对应边成比例列式整理可得AF•BE=AB•AD,从而得到AF=BE,再根据四边形EBHG是平行四边形且有一个角是直角即可证明四边形EBHG是正方形;
拓展延伸:把多边形先剖分成若干个三角形,把三角形剖分成矩形,把矩形剖分成正方形,把每两个正方形剖分成一个正方形,最后即可得解.
阅读解释:连接OI、NI,先利用相似三角形对应边成比例证明IM2=OM•NM,根据操作方法可得AF2=AB•AD,然后证明△DFA和△EAB相似,根据相似三角形对应边成比例列式整理可得AF•BE=AB•AD,从而得到AF=BE,再根据四边形EBHG是平行四边形且有一个角是直角即可证明四边形EBHG是正方形;
拓展延伸:把多边形先剖分成若干个三角形,把三角形剖分成矩形,把矩形剖分成正方形,把每两个正方形剖分成一个正方形,最后即可得解.
解答: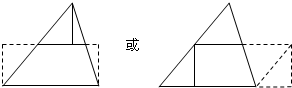 解:尝试操作,
解:尝试操作,
答案不唯一,如:
阅读解释
在辅助图中,连接OI、NI.
∵ON是所作半圆的直径,
∴∠OIN=90°.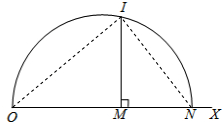
∵MI⊥ON,
∴∠OMI=∠IMN=90°且∠OIM=∠INM.
∴△OIM∽△INM.
∴
=
.
即IM2=OM•NM.…(3分)
在图4中,根据操作方法可知,AF2=AB•AD.
∵四边形ABCD是矩形,BE⊥AF,
∴DC∥AB,∠ADF=∠BEA=90°.
∴∠DFA=∠EAB.
∴△DFA∽△EAB.
∴
=
.
即AF•BE=AB•AD.(注:用面积法说明也可.)…(4分)
∴AF=BE.…(5分)
即BH=BE.
由操作方法知BE∥GH,BE=GH.
∴四边形EBHG是平行四边形.
∵∠GEB=90°,
∴四边形EBHG是正方形.…(6分)
拓展延伸
可以.采用以下剖分--重拼步骤:
(1)将多边形剖分为若干三角形;
(2)每个三角形剖分--重拼为一个矩形;
(3)每个矩形剖分--重拼为一个正方形;
(4)每两个正方形剖分--重拼为一个正方形.…(10分)
 解:尝试操作,
解:尝试操作,答案不唯一,如:
阅读解释
在辅助图中,连接OI、NI.
∵ON是所作半圆的直径,
∴∠OIN=90°.

∵MI⊥ON,
∴∠OMI=∠IMN=90°且∠OIM=∠INM.
∴△OIM∽△INM.
∴
| OM |
| IM |
| IM |
| NM |
即IM2=OM•NM.…(3分)
在图4中,根据操作方法可知,AF2=AB•AD.
∵四边形ABCD是矩形,BE⊥AF,
∴DC∥AB,∠ADF=∠BEA=90°.
∴∠DFA=∠EAB.
∴△DFA∽△EAB.
∴
| AD |
| BE |
| AF |
| AB |
即AF•BE=AB•AD.(注:用面积法说明也可.)…(4分)
∴AF=BE.…(5分)
即BH=BE.
由操作方法知BE∥GH,BE=GH.
∴四边形EBHG是平行四边形.
∵∠GEB=90°,
∴四边形EBHG是正方形.…(6分)
拓展延伸
可以.采用以下剖分--重拼步骤:
(1)将多边形剖分为若干三角形;
(2)每个三角形剖分--重拼为一个矩形;
(3)每个矩形剖分--重拼为一个正方形;
(4)每两个正方形剖分--重拼为一个正方形.…(10分)
点评:本题考查了利用轴对称作图,圆周角定理,相似三角形的判定与性质,读懂题目提供的信息并掌握利用是解题的关键.

练习册系列答案
相关题目
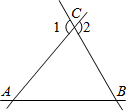 (2012•白下区一模)如图,三条直线两两相交,交点分别为A、B、C,若∠CAB=50°,∠CBA=60°,则∠1+∠2=
(2012•白下区一模)如图,三条直线两两相交,交点分别为A、B、C,若∠CAB=50°,∠CBA=60°,则∠1+∠2=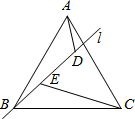 (2012•白下区一模)如图,直线l经过等边三角形ABC的顶点B,在l上取点D、E,使∠ADB=∠CEB=120°.若AD=2cm,CE=5cm,则DE=
(2012•白下区一模)如图,直线l经过等边三角形ABC的顶点B,在l上取点D、E,使∠ADB=∠CEB=120°.若AD=2cm,CE=5cm,则DE=