摘要:已知.在Rt△OAB中.∠OAB=900.∠BOA=300.AB=2.若以O为坐标原点.OA所在直线为轴.建立如图所示的平面直角坐标系.点B在第一象限内.将Rt△OAB沿OB折叠后.点A落在第一象限内的点C处. (1)求点C的坐标, (2)若抛物线(≠0)经过C.A两点.求此抛物线的解析式, (3)若抛物线的对称轴与OB交于点D.点P为线段DB上一点.过P作轴的平行线.交抛物线于点M.问:是否存在这样的点P.使得四边形CDPM为等腰梯形?若存在.请求出此时点P的坐标,若不存在.请说明理由. 注:抛物线(≠0)的顶点坐标为.对称轴公式为 解:(1)过点C作CH⊥轴.垂足为H ∵在Rt△OAB中.∠OAB=900.∠BOA=300.AB=2 ∴OB=4.OA= 由折叠知.∠COB=300.OC=OA= ∴∠COH=600.OH=.CH=3 ∴C点坐标为(.3) (2)∵抛物线(≠0)经过C(.3).A(.0)两点 ∴ 解得: ∴此抛物线的解析式为: (3)存在.因为的顶点坐标为(.3)即为点C MP⊥轴.设垂足为N.PN=.因为∠BOA=300.所以ON= ∴P(.) 作PQ⊥CD.垂足为Q.ME⊥CD.垂足为E 把代入得: ∴ M(.).E(.) 同理:Q(.).D(.1) 要使四边形CDPM为等腰梯形.只需CE=QD 即.解得:.(舍) ∴ P点坐标为(.) ∴ 存在满足条件的点P.使得四边形CDPM为等腰梯形.此时P点的坐为(.)
网址:http://m.1010jiajiao.com/timu3_id_463208[举报]
 (2013•六盘水)已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2
(2013•六盘水)已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2| 3 |
(1)求经过点O,C,A三点的抛物线的解析式.
(2)求抛物线的对称轴与线段OB交点D的坐标.
(3)线段OB与抛物线交与点E,点P为线段OE上一动点(点P不与点O,点E重合),过P点作y轴的平行线,交抛物线于点M,问:在线段OE上是否存在这样的点P,使得PD=CM?若存在,请求出此时点P的坐标;若不存在,请说明理由.
已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直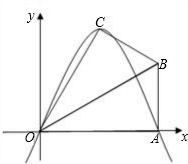 线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作y轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. 查看习题详情和答案>>
 线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作y轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. 查看习题详情和答案>>
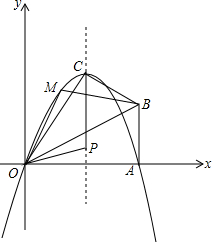 (2013•武汉模拟)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 为原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(2013•武汉模拟)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 为原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.(1)求点C的坐标和过O、C、A三点的抛物线的解析式;
(2)P是此抛物线的对称轴上一动点,当以P、O、C为顶点的三角形是等腰三角形时,请直接写出点P的坐标;
(3)M(x,y)是此抛物线上一个动点,当△MOB的面积等于△OAB面积时,求M的坐标.
已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M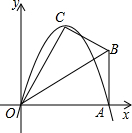 .问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
,
),对称轴公式为x=-
.
查看习题详情和答案>>
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M
 .问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
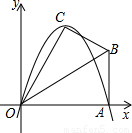
(2007•重庆)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为 ,对称轴公式为x=-
,对称轴公式为x=- .
.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为
 ,对称轴公式为x=-
,对称轴公式为x=- .
. 查看习题详情和答案>>
查看习题详情和答案>>