ÌâÄ¿ÄÚÈÝ
 £¨2013•ÁùÅÌË®£©ÒÑÖª£®ÔÚRt¡÷OABÖУ¬¡ÏOAB=90¡ã£¬¡ÏBOA=30¡ã£¬OA=2
£¨2013•ÁùÅÌË®£©ÒÑÖª£®ÔÚRt¡÷OABÖУ¬¡ÏOAB=90¡ã£¬¡ÏBOA=30¡ã£¬OA=2| 3 |
£¨1£©Çó¾¹ýµãO£¬C£¬AÈýµãµÄÅ×ÎïÏߵĽâÎöʽ£®
£¨2£©ÇóÅ×ÎïÏߵĶԳÆÖáÓëÏ߶ÎOB½»µãDµÄ×ø±ê£®
£¨3£©Ï߶ÎOBÓëÅ×ÎïÏß½»ÓëµãE£¬µãPΪÏ߶ÎOEÉÏÒ»¶¯µã£¨µãP²»ÓëµãO£¬µãEÖغϣ©£¬¹ýPµã×÷yÖáµÄƽÐÐÏߣ¬½»Å×ÎïÏßÓÚµãM£¬ÎÊ£ºÔÚÏ߶ÎOEÉÏÊÇ·ñ´æÔÚÕâÑùµÄµãP£¬Ê¹µÃPD=CM£¿Èô´æÔÚ£¬ÇëÇó³ö´ËʱµãPµÄ×ø±ê£»Èô²»´æÔÚ£¬Çë˵Ã÷ÀíÓÉ£®
·ÖÎö£º£¨1£©ÔÚRt¡÷AOBÖУ¬¸ù¾ÝAOµÄ³¤ºÍ¡ÏBOAµÄ¶ÈÊý£¬¿ÉÇóµÃOBµÄ³¤£¬¸ù¾ÝÕÛµþµÄÐÔÖʼ´¿ÉµÃµ½OA=OC£¬ÇÒ¡ÏBOC=¡ÏBOA=30¡ã£¬¹ýC×÷CD¡ÍxÖáÓÚD£¬¼´¿É¸ù¾Ý¡ÏCODµÄ¶ÈÊýºÍOCµÄ³¤ÇóµÃCD¡¢ODµÄÖµ£¬´Ó¶øÇó³öµãC¡¢AµÄ×ø±ê£¬½«A¡¢C¡¢OµÄ×ø±ê´úÈëÅ×ÎïÏߵĽâÎöʽÖУ¬Í¨¹ýÁªÁ¢·½³Ì×é¼´¿ÉÇó³ö´ý¶¨ÏµÊýµÄÖµ£¬´Ó¶øÈ·¶¨¸ÃÅ×ÎïÏߵĽâÎöʽ£®
£¨2£©Çó³öÖ±ÏßBOµÄ½âÎöʽ£¬½ø¶øÀûÓÃx=
Çó³öyµÄÖµ£¬¼´¿ÉµÃ³öDµã×ø±ê£»
£¨3£©¸ù¾Ý£¨1£©ËùµÃÅ×ÎïÏߵĽâÎöʽ¿ÉµÃµ½Æ䶥µãµÄ×ø±ê£¨¼´Cµã£©£¬ÉèÖ±ÏßMPÓëxÖáµÄ½»µãΪN£¬ÇÒPN=t£¬ÔÚRt¡÷OPNÖУ¬¸ù¾Ý¡ÏPONµÄ¶ÈÊý£¬Ò×µÃPN¡¢ONµÄ³¤£¬¼´¿ÉµÃµ½µãPµÄ×ø±ê£¬È»ºó¸ù¾ÝµãPµÄºá×ø±êºÍÅ×ÎïÏߵĽâÎöʽ¿ÉÇóµÃMµãµÄ×Ý×ø±ê£¬¹ýM×÷MF¡ÍCD£¨¼´Å×ÎïÏ߶ԳÆÖᣩÓÚF£¬¹ýP×÷PQ¡ÍCDÓÚQ£¬ÈôPD=CM£¬ÄÇôCF=QD£¬¸ù¾ÝC¡¢M¡¢P¡¢DËĵã×Ý×ø±ê£¬Ò×ÇóµÃCF¡¢QDµÄ³¤£¬ÁªÁ¢Á½Ê½¼´¿ÉÇó³ö´ËʱtµÄÖµ£¬´Ó¶øÇóµÃµãPµÄ×ø±ê£®
£¨2£©Çó³öÖ±ÏßBOµÄ½âÎöʽ£¬½ø¶øÀûÓÃx=
| 3 |
£¨3£©¸ù¾Ý£¨1£©ËùµÃÅ×ÎïÏߵĽâÎöʽ¿ÉµÃµ½Æ䶥µãµÄ×ø±ê£¨¼´Cµã£©£¬ÉèÖ±ÏßMPÓëxÖáµÄ½»µãΪN£¬ÇÒPN=t£¬ÔÚRt¡÷OPNÖУ¬¸ù¾Ý¡ÏPONµÄ¶ÈÊý£¬Ò×µÃPN¡¢ONµÄ³¤£¬¼´¿ÉµÃµ½µãPµÄ×ø±ê£¬È»ºó¸ù¾ÝµãPµÄºá×ø±êºÍÅ×ÎïÏߵĽâÎöʽ¿ÉÇóµÃMµãµÄ×Ý×ø±ê£¬¹ýM×÷MF¡ÍCD£¨¼´Å×ÎïÏ߶ԳÆÖᣩÓÚF£¬¹ýP×÷PQ¡ÍCDÓÚQ£¬ÈôPD=CM£¬ÄÇôCF=QD£¬¸ù¾ÝC¡¢M¡¢P¡¢DËĵã×Ý×ø±ê£¬Ò×ÇóµÃCF¡¢QDµÄ³¤£¬ÁªÁ¢Á½Ê½¼´¿ÉÇó³ö´ËʱtµÄÖµ£¬´Ó¶øÇóµÃµãPµÄ×ø±ê£®
½â´ð£º ½â£º£¨1£©¹ýµãC×÷CH¡ÍxÖᣬ´¹×ãΪH£»
½â£º£¨1£©¹ýµãC×÷CH¡ÍxÖᣬ´¹×ãΪH£»
¡ßÔÚRt¡÷OABÖУ¬¡ÏOAB=90¡ã£¬¡ÏBOA=30¡ã£¬OA=2
£¬
¡àOB=
=4£¬AB=2£»
ÓÉÕÛµþµÄÐÔÖÊÖª£º¡ÏCOB=30¡ã£¬OC=AO=2
£¬
¡à¡ÏCOH=60¡ã£¬OH=
£¬CH=3£»
¡àCµã×ø±êΪ£¨
£¬3£©£®
¡ßOµã×ø±êΪ£º£¨0£¬0£©£¬
¡àÅ×ÎïÏß½âÎöʽΪy=ax2+bx£¨a¡Ù0£©£¬
¡ßͼÏó¾¹ýC£¨
£¬3£©¡¢A£¨2
£¬0£©Á½µã£¬
¡à
£¬
½âµÃ
£»
¡à´ËÅ×ÎïÏߵĺ¯Êý¹ØϵʽΪ£ºy=-x2+2
x£®
£¨2£©¡ßAO=2
£¬AB=2£¬
¡àBµã×ø±êΪ£º£¨2
£¬2£©£¬
¡àÉèÖ±ÏßBOµÄ½âÎöʽΪ£ºy=kx£¬
Ôò2=2
k£¬
½âµÃ£ºk=
£¬
¡ày=
x£¬
¡ßy=-x2+2
xµÄ¶Ô³ÆÖáΪֱÏßx=-
=-
=
£¬
¡à½«Á½º¯ÊýÁªÁ¢µÃ³ö£ºy=
¡Á
=1£¬
¡àÅ×ÎïÏߵĶԳÆÖáÓëÏ߶ÎOB½»µãDµÄ×ø±êΪ£º£¨
£¬1£©£»
£¨3£©´æÔÚ£®
¡ßy=-x2+2
xµÄ¶¥µã×ø±êΪ£¨
£¬3£©£¬
¼´ÎªµãC£¬MP¡ÍxÖᣬ´¹×ãΪN£¬ÉèPN=t£»
¡ß¡ÏBOA=30¡ã£¬
¡àON=
t£¬
¡àP£¨
t£¬t£©£»
×÷PQ¡ÍCD£¬´¹×ãΪQ£¬MF¡ÍCD£¬´¹×ãΪF£»
°Ñx=
t´úÈëy=-x2+2
x£¬
µÃy=-3t2+6t£¬
¡àM£¨
t£¬-3t2+6t£©£¬F£¨
£¬-3t2+6t£©£¬
ͬÀí£ºQ£¨
£¬t£©£¬D£¨
£¬1£©£»
ҪʹPD=CM£¬Ö»ÐèCF=QD£¬
¼´3-£¨-3t2+6t£©=|t-1|£¬
½âµÃt=
£¬t=1£¨Éᣩ£¬t=
£¬
¡àPµã×ø±êΪ£¨
£¬
£©£¬»ò£¨
£¬
£©£¬
¡à´æÔÚÂú×ãÌõ¼þµÄPµã£¬Ê¹µÃPD=CM£¬´ËʱPµã×ø±êΪ£¨
£¬
£©»ò£¨
£¬
£©£®
 ½â£º£¨1£©¹ýµãC×÷CH¡ÍxÖᣬ´¹×ãΪH£»
½â£º£¨1£©¹ýµãC×÷CH¡ÍxÖᣬ´¹×ãΪH£»¡ßÔÚRt¡÷OABÖУ¬¡ÏOAB=90¡ã£¬¡ÏBOA=30¡ã£¬OA=2
| 3 |
¡àOB=
| cos30¡ã |
| AO |
ÓÉÕÛµþµÄÐÔÖÊÖª£º¡ÏCOB=30¡ã£¬OC=AO=2
| 3 |
¡à¡ÏCOH=60¡ã£¬OH=
| 3 |
¡àCµã×ø±êΪ£¨
| 3 |
¡ßOµã×ø±êΪ£º£¨0£¬0£©£¬
¡àÅ×ÎïÏß½âÎöʽΪy=ax2+bx£¨a¡Ù0£©£¬
¡ßͼÏó¾¹ýC£¨
| 3 |
| 3 |
¡à
|
½âµÃ
|
¡à´ËÅ×ÎïÏߵĺ¯Êý¹ØϵʽΪ£ºy=-x2+2
| 3 |
£¨2£©¡ßAO=2
| 3 |
¡àBµã×ø±êΪ£º£¨2
| 3 |
¡àÉèÖ±ÏßBOµÄ½âÎöʽΪ£ºy=kx£¬
Ôò2=2
| 3 |
½âµÃ£ºk=
| ||
| 3 |
¡ày=
| ||
| 3 |
¡ßy=-x2+2
| 3 |
| b |
| 2a |
2
| ||
| 2¡Á(-1) |
| 3 |
¡à½«Á½º¯ÊýÁªÁ¢µÃ³ö£ºy=
| ||
| 3 |
| 3 |
¡àÅ×ÎïÏߵĶԳÆÖáÓëÏ߶ÎOB½»µãDµÄ×ø±êΪ£º£¨
| 3 |
£¨3£©´æÔÚ£®
¡ßy=-x2+2
| 3 |
| 3 |
¼´ÎªµãC£¬MP¡ÍxÖᣬ´¹×ãΪN£¬ÉèPN=t£»
¡ß¡ÏBOA=30¡ã£¬
¡àON=
| 3 |
¡àP£¨
| 3 |
×÷PQ¡ÍCD£¬´¹×ãΪQ£¬MF¡ÍCD£¬´¹×ãΪF£»
°Ñx=
| 3 |
| 3 |
µÃy=-3t2+6t£¬
¡àM£¨
| 3 |
| 3 |
ͬÀí£ºQ£¨
| 3 |
| 3 |
ҪʹPD=CM£¬Ö»ÐèCF=QD£¬
¼´3-£¨-3t2+6t£©=|t-1|£¬
½âµÃt=
| 4 |
| 3 |
| 2 |
| 3 |
¡àPµã×ø±êΪ£¨
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
¡à´æÔÚÂú×ãÌõ¼þµÄPµã£¬Ê¹µÃPD=CM£¬´ËʱPµã×ø±êΪ£¨
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
µãÆÀ£º´ËÌâÖ÷Òª¿¼²éÁËͼÐεÄÐýת±ä»¯¡¢½âÖ±½ÇÈý½ÇÐΡ¢¶þ´Îº¯Êý½âÎöʽµÄÈ·¶¨µÈÖØҪ֪ʶµã£¬±íʾ³öPµã×ø±êÀûÓÃCF=QDÇó³öÊǽâÌâ¹Ø¼ü£®

Á·Ï°²áϵÁдð°¸
 ÔĶÁ¿ì³µÏµÁдð°¸
ÔĶÁ¿ì³µÏµÁдð°¸
Ïà¹ØÌâÄ¿
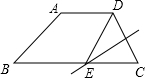 £¨2013•ÁùÅÌË®£©Èçͼ£¬ÌÝÐÎABCDÖУ¬AD¡ÎBC£¬AD=4£¬AB=5£¬BC=10£¬CDµÄ´¹Ö±Æ½·ÖÏß½»BCÓÚE£¬Á¬½ÓDE£¬ÔòËıßÐÎABEDµÄÖܳ¤µÈÓÚ
£¨2013•ÁùÅÌË®£©Èçͼ£¬ÌÝÐÎABCDÖУ¬AD¡ÎBC£¬AD=4£¬AB=5£¬BC=10£¬CDµÄ´¹Ö±Æ½·ÖÏß½»BCÓÚE£¬Á¬½ÓDE£¬ÔòËıßÐÎABEDµÄÖܳ¤µÈÓÚ