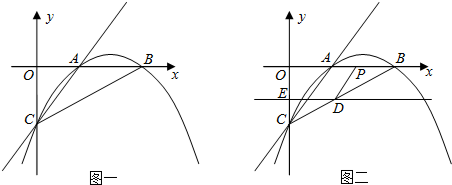
（2012•鄂州）已知：如图一，抛物线y=ax²+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x-2经过A、C两点，且AB=2．
（1）求抛物线的解析式；
（2）若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s=

ED+OP

ED•OP

，当t为何值时，s有最小值，并求出最小值．
（3）在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．

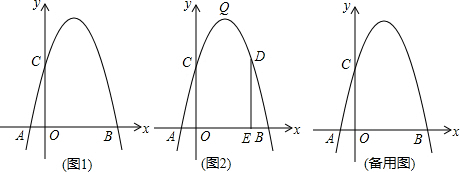
（2013•大安市模拟）已知：如图1，抛物线y=-x²+bx+c的顶点为Q，与x轴交于A（-1，0）、B（5，0）两点，与y轴交于C点．
（1）求抛物线的解析式及其顶点Q的坐标；
（2）在该抛物线的对称轴上求一点P，使得△PAC的周长最小．请在图中画出点P的位置，并求点P的坐标；
（3）如图2，若点D是第一象限抛物线上的一个动点，过D作DE⊥x轴，垂足为E．
①有一个同学说：“在第一象限抛物线上的所有点中，抛物线的顶点Q与x轴相距最远，所以当点D运动至点Q时，折线D-E-O的长度最长”．这个同学的说法正确吗？请说明理由．
②若DE与直线BC交于点F．试探究：四边形DCEB能否为平行四边形？若能，请直接写出点D的坐标；若不能，请简要说明理由；

（2013•宝安区二模）已知：如图1，抛物线经过点O、A、B三点，四边形OABC是直角梯形，其中点A在x轴上，点C在y轴上，BC∥OA，A（12，0）、B（4，8）．
（1）求抛物线所对应的函数关系式；
（2）若D为OA的中点，动点P自A点出发沿A→B→C→O的路线移动，速度为每秒1个单位，移动时间记为t秒．几秒钟后线段PD将梯形OABC的面积分成1﹕3两部分？并求出此时P点的坐标；
（3）如图2，作△OBC的外接圆O′，点Q是抛物线上点A、B之间的动点，连接OQ交⊙O′于点M，交AB于点N．当∠BOQ=45°时，求线段MN的长．