题目内容
已知,如图1,抛物线y=ax2+bx过点A(6,3),且对称轴为直线x=| 5 | 2 |
(1)求该抛物线的解析式;
(2)若△OAB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)如图2,过点B作直线BC∥y轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使△BCD是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标;若不存在,请说明理由.

分析:(1)根据抛物线y=ax2+bx过点A(6,3),且对称轴为直线x=
,利用待定系数法求解即可;
(2)过点B作BH∥y轴,交OA于点H,将△OAB分成△OBH和△ABH两部分求解;
(3)假设存在满足题意的D点,再根据△BCD是以D为直角顶点的等腰直角三角形这一条件解答.
| 5 |
| 2 |
(2)过点B作BH∥y轴,交OA于点H,将△OAB分成△OBH和△ABH两部分求解;
(3)假设存在满足题意的D点,再根据△BCD是以D为直角顶点的等腰直角三角形这一条件解答.
解答:解:(1)由题知:
解之,得
,
∴该抛物线的解析式为:y=
x2-
x.
(2)过点B作BH∥y轴,交OA于点H,
由题知直线OA为:y=
x,
∴设点H(m,
m),点B(m,
m2-
m),∴BH=
m-(
m2-
m)=-
m2+3m,
∴S=S△OBH+S△ABH=
BH×6=
(-
m2+3m)×6=-
m2+9m,
=-
(m-3)2+
(0<m<6),
∴当m=3时,S最大=
;
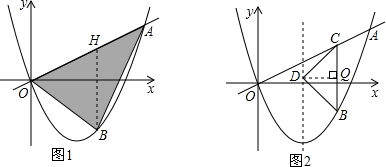
(3)存在,点B为(1+
,
)或(5-
,
),
理由如下:设在抛物线的对称轴(x=
)上存在点D满足题意,
过点D作DQ⊥BC于点Q,
则由(2)有点C(m,
m),点B(m,
m2-
m),BC=-
m2+3m
∵△BCD是以D为直角顶点的等腰直角三角形
∴DQ=
BC,即是:|m-
|=
(-
m2+3m)且(0<m<6),
若m-
=
(-
m2+3m),解之:m1=1-
(舍去),m2=1+
,
当m2=1+
时,y=
(1+
)2-
(1+
)=
,
∴点B(1+
,
),
若
-m=
(-
m2,+3m),解之:m3=5-
,m4=5+
(舍去),
当m3=5-
时,y=
(5-
)2-
(5-
)=
,
∴点B为(5-
,
),
综上,满足条件的点B为(1+
,
)或(5-
,
).
|
|
∴该抛物线的解析式为:y=
| 1 |
| 2 |
| 5 |
| 2 |
(2)过点B作BH∥y轴,交OA于点H,
由题知直线OA为:y=
| 1 |
| 2 |
∴设点H(m,
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∴S=S△OBH+S△ABH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 27 |
| 2 |
∴当m=3时,S最大=
| 27 |
| 2 |

(3)存在,点B为(1+
| 11 |
7-3
| ||
| 2 |
| 15 |
15-5
| ||
| 2 |
理由如下:设在抛物线的对称轴(x=
| 5 |
| 2 |
过点D作DQ⊥BC于点Q,
则由(2)有点C(m,
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∵△BCD是以D为直角顶点的等腰直角三角形
∴DQ=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
若m-
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 11 |
当m2=1+
| 11 |
| 1 |
| 2 |
| 11 |
| 5 |
| 2 |
| 11 |
7-3
| ||
| 2 |
∴点B(1+
| 11 |
7-3
| ||
| 2 |
若
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 15 |
当m3=5-
| 15 |
| 1 |
| 2 |
| 15 |
| 5 |
| 2 |
| 15 |
15-5
| ||
| 2 |
∴点B为(5-
| 15 |
15-5
| ||
| 2 |
综上,满足条件的点B为(1+
| 11 |
7-3
| ||
| 2 |
| 15 |
15-5
| ||
| 2 |
点评:本题考查了二次函数的知识,是一道综合题,难度较大,需要对各部分知识熟练掌握并灵活应用.

练习册系列答案
相关题目