题目内容
(2013•宝安区二模)已知:如图1,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(1)求抛物线所对应的函数关系式;
(2)若D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒.几秒钟后线段PD将梯形OABC的面积分成1﹕3两部分?并求出此时P点的坐标;
(3)如图2,作△OBC的外接圆O′,点Q是抛物线上点A、B之间的动点,连接OQ交⊙O′于点M,交AB于点N.当∠BOQ=45°时,求线段MN的长.

(1)求抛物线所对应的函数关系式;
(2)若D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒.几秒钟后线段PD将梯形OABC的面积分成1﹕3两部分?并求出此时P点的坐标;
(3)如图2,作△OBC的外接圆O′,点Q是抛物线上点A、B之间的动点,连接OQ交⊙O′于点M,交AB于点N.当∠BOQ=45°时,求线段MN的长.

分析:(1)根据抛物线经过原点,设抛物线解析式为y=ax2+bx(a≠0),然后把点A、B的坐标代入求出a、b的值,即可得解;
(2)先求出梯形OABC的面积为64和AB的长,再求出两个部分的面积分别为16和48,然后分△ADP的面积是16时,过点P作PE⊥x轴于E,根据等腰直角三角形的性质求出PE的长,再根据三角形的面积列式计算即可得解;△PDO的面积是16时,求出OP的长,再列式求解即可;
(3)先利用勾股定理列式求出OB,再根据两组角对应相等的两个三角形相似可得△AOB和△ONB相似,利用相似三角形对应边成比例列式求出ON的长,连接BM,判断出△OBM是等腰直角三角形,根据等腰直角三角形的性质求出OM,再根据MN=ON-OM计算即可得解.
(2)先求出梯形OABC的面积为64和AB的长,再求出两个部分的面积分别为16和48,然后分△ADP的面积是16时,过点P作PE⊥x轴于E,根据等腰直角三角形的性质求出PE的长,再根据三角形的面积列式计算即可得解;△PDO的面积是16时,求出OP的长,再列式求解即可;
(3)先利用勾股定理列式求出OB,再根据两组角对应相等的两个三角形相似可得△AOB和△ONB相似,利用相似三角形对应边成比例列式求出ON的长,连接BM,判断出△OBM是等腰直角三角形,根据等腰直角三角形的性质求出OM,再根据MN=ON-OM计算即可得解.
解答:解:(1)∵抛物线经过点A(12,0)、B(4,8)和原点O,
∴设抛物线解析式为y=ax2+bx(a≠0),
则
,
解得
,
∴抛物线所对应的函数关系式为y=-
x2+3x;
(2)∵A(12,0),B(4,8),BC∥OA,
∴OA=12,BC=4,OC=8,∠OAB=45°,
∴梯形OABC的面积=
×(4+12)×8=64,
∵AD是OA的中点,
∴OD=AD=
OA=
×12=6,
∵线段PD将梯形OABC的面积分成1:3两部分,
∴分成两部分的面积分别为64×
=16,
64×
=48,
如图1,△ADP的面积是16时,过点P作PE⊥x轴于E,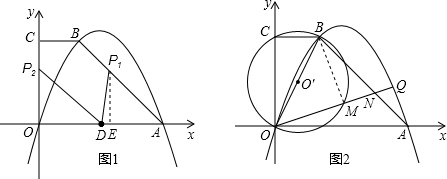
∵AP=t,
∴PE=
t,
∴
×6×
t=16,
解得t=
,
∴PE=
×
=
,
OE=12-
×
=
,
∴点P(
,
),
△PDO的面积是16时,
×6•OP=16,
解得OP=
,
∵AB=
=8
,
∴t=(AB+BC+OC-OP)÷1=8
+4+8-
=8
+
,
此时,点P(0,
),
综上所述,
秒或8
+
秒钟后线段PD将梯形OABC的面积分成1:3两部分,
此时P点的坐标为(
,
)或(0,
);
(3)在Rt△OBC中,由勾股定理得,OB=
=
=4
,
∵∠OAB=45°,∠BOQ=45°,
∴∠OAB=∠BOQ,
又∵∠ABO=∠OBN,
∴△AOB∽△ONB,
∴
=
,
即
=
,
解得ON=3
,
如图2,连接BM,∵∠BOQ=45°,OB是⊙O′的直径,
∴△OBM是等腰直角三角形,
∴OM=
OB=
×4
=2
,
∴MN=ON-OM=3
-2
=
.
∴设抛物线解析式为y=ax2+bx(a≠0),
则
|
解得
|
∴抛物线所对应的函数关系式为y=-
| 1 |
| 4 |
(2)∵A(12,0),B(4,8),BC∥OA,
∴OA=12,BC=4,OC=8,∠OAB=45°,
∴梯形OABC的面积=
| 1 |
| 2 |
∵AD是OA的中点,
∴OD=AD=
| 1 |
| 2 |
| 1 |
| 2 |
∵线段PD将梯形OABC的面积分成1:3两部分,
∴分成两部分的面积分别为64×
| 1 |
| 1+3 |
64×
| 3 |
| 1+3 |
如图1,△ADP的面积是16时,过点P作PE⊥x轴于E,
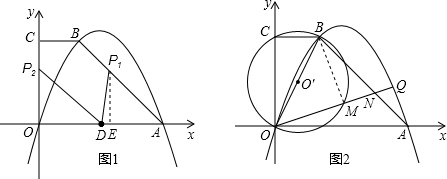
∵AP=t,
∴PE=
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
解得t=
16
| ||
| 3 |
∴PE=
16
| ||
| 3 |
| ||
| 2 |
| 16 |
| 3 |
OE=12-
16
| ||
| 3 |
| ||
| 2 |
| 20 |
| 3 |
∴点P(
| 20 |
| 3 |
| 16 |
| 3 |
△PDO的面积是16时,
| 1 |
| 2 |
解得OP=
| 16 |
| 3 |
∵AB=
| 82+(12-4)2 |
| 2 |
∴t=(AB+BC+OC-OP)÷1=8
| 2 |
| 16 |
| 3 |
| 2 |
| 20 |
| 3 |
此时,点P(0,
| 16 |
| 3 |
综上所述,
16
| ||
| 3 |
| 2 |
| 20 |
| 3 |
此时P点的坐标为(
| 20 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
(3)在Rt△OBC中,由勾股定理得,OB=
| OC2+BC2 |
| 82+42 |
| 5 |
∵∠OAB=45°,∠BOQ=45°,
∴∠OAB=∠BOQ,
又∵∠ABO=∠OBN,
∴△AOB∽△ONB,
∴
| ON |
| AO |
| OB |
| AB |
即
| ON |
| 12 |
4
| ||
8
|
解得ON=3
| 10 |
如图2,连接BM,∵∠BOQ=45°,OB是⊙O′的直径,
∴△OBM是等腰直角三角形,
∴OM=
| ||
| 2 |
| ||
| 2 |
| 5 |
| 10 |
∴MN=ON-OM=3
| 10 |
| 10 |
| 10 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,三角形的面积,相似三角形的判定与性质,(2)难点在于要根据点P的位置分情况讨论,(3)判断出两个三角形相似是解题的关键.

练习册系列答案
相关题目
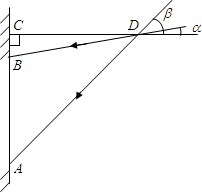 (2013•宝安区二模)在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )
(2013•宝安区二模)在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( ) (2013•宝安区二模)如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长=
(2013•宝安区二模)如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长=