摘要：如图11-2.若△ABC绕着点A旋转一定角度就得到△ADE.那么AB= .∠ACB= .点B与点 对应.
网址：http://m.1010jiajiao.com/timu3_id_456650[举报]
27、如图所示，若△ABC、△ADE都是正三角形，请试比较：线段BD与线段CE的大小？写出你的猜想，并说明理由．
如图所示，若△ABC≌△EFC，且CF=3厘米，∠EFC=64°，则BC=
9、如图所示，若△ABC∽△DEF，则∠E的度数为（ ）请完成下面的说明：
（1）如图①所示，△ABC的外角平分线交于G，试说明∠BGC=90°-
∠A．
说明：根据三角形内角和等于180°，可知∠ABC+∠ACB=180°-∠
根据平角是180°，可知∠ABE+∠ACF=180°×2=360°，
所以∠EBC+∠FCB=360°-（∠ABC+∠ACB）=360°-（180°-∠
(∠EBC+∠FCB)=
(180°+∠
∠
∠
（2）如图②所示，若△ABC的内角平分线交于点I，试说明∠BIG=90°+
∠A．
（3）用（1），（2）的结论，你能说出∠BGC和∠BIC的关系吗？
查看习题详情和答案>>
（1）如图①所示，△ABC的外角平分线交于G，试说明∠BGC=90°-
| 1 |
| 2 |
说明：根据三角形内角和等于180°，可知∠ABC+∠ACB=180°-∠
A
A
．根据平角是180°，可知∠ABE+∠ACF=180°×2=360°，
所以∠EBC+∠FCB=360°-（∠ABC+∠ACB）=360°-（180°-∠
A
A
）=180°+∠A
A
．根据角平分线的意义，可知∠2+∠3=| 1 |
| 2 |
| 1 |
| 2 |
A
A
）=90°+| 1 |
| 2 |
A
A
．所以∠BGC=180°-(∠2+∠3)=90°-| 1 |
| 2 |
A
A
．（2）如图②所示，若△ABC的内角平分线交于点I，试说明∠BIG=90°+
| 1 |
| 2 |
（3）用（1），（2）的结论，你能说出∠BGC和∠BIC的关系吗？
课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：
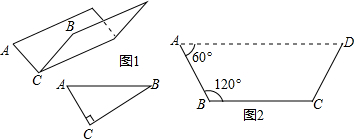
（1）方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米2，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小；
（2）假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．
查看习题详情和答案>>
初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：
（1）方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米2，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小；
（2）假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．
查看习题详情和答案>>