摘要： 解:如图.根据题意.有AB∥CD.PM⊥CD于N点. 交AB于M点.且AB=20m. CD=50m. PM=25m. AB∥CD→△PAB∽△PCD→ → →PN=62.5→MN=37.5
网址：http://m.1010jiajiao.com/timu3_id_456604[举报]
考点：作图—复杂作图。
专题：作图题。
分析：设正方形的面积为2，则△BEC的面积为1，根据题意，分成的每一个直角梯形的面积为
，然后找出正方形的中心O，过中心O分别作OF∥AD交AB于点F、作OG∥CD交BE于点H，交BC边于点G，连接OD、HE，即可作出．
解答：解：如图所示，①②③④部分就是全等的直角梯形．
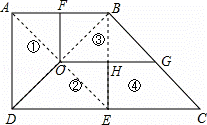
点评：本题主要考查了复杂作图，根据面积确定出从正方形的中心入手求解是解题的关键，难度中等，但不容易考虑．
查看习题详情和答案>>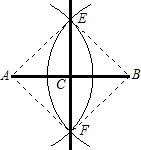
阅读并填空：如图：根据六年级第二学期学过的用直尺、圆规作线段中点的方法，画出了线段AB的中点C，请说明这种方法正确的理由．
解：连接AE、BE、AF、BF．
在△AEF和△BEF中，
EF=EF（
所以△AEF≌△BEF （
所以∠AEF=∠BEF （
又AE=BE，
所以AC=BC （
即点C是线段AB的中点． 查看习题详情和答案>>
（2010•保定一模）如图，A、B、C分别表示面积为9、10、11的三个圆．已知三个圆所覆盖的总面积为20．A与B、B与C、C与A每两圆公共部分所覆盖面积分别为5、4、3，求A、B、C三个圆公共部分所覆盖的面积．
探索发现：
我们把三个圆所覆盖的总面积记为A∨B∨C；每两圆公共部分所覆盖的面积记为AB、BC、CA；三个圆公共部分所覆盖的面积记为ABC．根据题意，有：
（1）三个圆的面积和为：A+B+C=
（2）重合部分覆盖的面积为（A+B+C）-A∨B∨C=
（3）每两圆公告部分所覆盖的面积和为：AB+BC+CA=
（4）三个圆公共部分所覆盖的面积：ABC=
总结归纳：
利用上题中规定的符号和解答过程，补全等式：ABC=
利用上述方法得到的启示，解决下面的问题：
某年级共有74名学生参加课外小组．其中，参加球类的有34人，参加棋类的有32人，参加田径类的有30人；既参加球类又参加棋类的有7人，既参加棋类又参加田径类的有8人，既参加田径类又参加球类的有10人．求三个小组都参加的人数．
查看习题详情和答案>>
探索发现：
我们把三个圆所覆盖的总面积记为A∨B∨C；每两圆公共部分所覆盖的面积记为AB、BC、CA；三个圆公共部分所覆盖的面积记为ABC．根据题意，有：
（1）三个圆的面积和为：A+B+C=
30
30
；（2）重合部分覆盖的面积为（A+B+C）-A∨B∨C=
10
10
；（3）每两圆公告部分所覆盖的面积和为：AB+BC+CA=
12
12
；（4）三个圆公共部分所覆盖的面积：ABC=
2
2
．总结归纳：
利用上题中规定的符号和解答过程，补全等式：ABC=
AB+BC+CA+A∨B∨C-（A+B+C）
AB+BC+CA+A∨B∨C-（A+B+C）
．利用上述方法得到的启示，解决下面的问题：
某年级共有74名学生参加课外小组．其中，参加球类的有34人，参加棋类的有32人，参加田径类的有30人；既参加球类又参加棋类的有7人，既参加棋类又参加田径类的有8人，既参加田径类又参加球类的有10人．求三个小组都参加的人数．
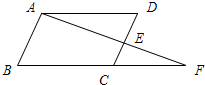24、如图，根据图形填空：