摘要: 已知.Rt△AOB中.∠AOB=90°.OA=3cm.OB=4cm.以O为坐标原点建立如图所示的平面直角坐标系.设P.Q分别为AB边.OB边上的动点.它们同时分别从点A.O向B点匀速运动.移动的速度为1cm/s.设P.Q移动时间为ts. (1)过点P作PM⊥OA于M.证明. 并求出点P的坐标. (2)求△OPQ的面积S(cm2)与移动时间t(s)之间的函数关系式,当t为何值时.S有最大值.并求出S的最大值. (3)请你探索:当t为何值时.△OPQ为直角三角形.
网址:http://m.1010jiajiao.com/timu3_id_456478[举报]
下列说法
①如图1,扇形OAB的圆心角∠AOB=90°,OA=6,点C是
上异于A、B的动点,过点C作CD⊥OA于D,作CE⊥OB于E,连接DE,点G在线段DE上,且DG=
DE,连接CG.当点C在
上运动时,在CD、CG、DG中,长度不变的是DG;
②如图2,正方形纸片ABCD的边长为8,⊙O的半径为2,圆心O在正方形的中心上,将纸片按图示方式折叠,折叠后点A于点H重合,且EH切⊙O于点H,延长FH交CD边于点G,则HG的长为
;
③已知Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则其内心和外心之间的距离是
cm.
其中正确的有

查看习题详情和答案>>
①如图1,扇形OAB的圆心角∠AOB=90°,OA=6,点C是
 |
| AB |
| 1 |
| 3 |
 |
| AB |
②如图2,正方形纸片ABCD的边长为8,⊙O的半径为2,圆心O在正方形的中心上,将纸片按图示方式折叠,折叠后点A于点H重合,且EH切⊙O于点H,延长FH交CD边于点G,则HG的长为
| 19 |
| 3 |
③已知Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则其内心和外心之间的距离是
| 5 |
其中正确的有
①②
①②
(请写序号,少选,错选均不得分)
已知Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以O为坐标原点建立如图所示的直角坐标系,设P、Q分别为AB、OB边上的动点,他们同时分别从点A、O向B点匀速移动,移动的速度都是1厘米/秒,设P、Q移动时间为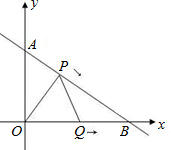 t秒(0≤t≤4)
t秒(0≤t≤4)
(1)试用t的代数式表示P点的坐标;
(2)求△OPQ的面积S(cm2)与t(秒)的函数关系式;当t为何值时,S有最大值,并求出S的最大值;
(3)试问是否存在这样的时刻t,使△OPQ为直角三角形?如果存在,求出t的值,如果不存在,请说明理由. 查看习题详情和答案>>
 t秒(0≤t≤4)
t秒(0≤t≤4)(1)试用t的代数式表示P点的坐标;
(2)求△OPQ的面积S(cm2)与t(秒)的函数关系式;当t为何值时,S有最大值,并求出S的最大值;
(3)试问是否存在这样的时刻t,使△OPQ为直角三角形?如果存在,求出t的值,如果不存在,请说明理由. 查看习题详情和答案>>
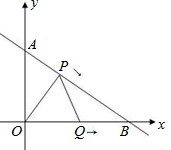 t秒(0≤t≤4)
t秒(0≤t≤4)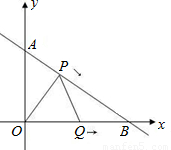
 t秒(0≤t≤4)
t秒(0≤t≤4)