题目内容
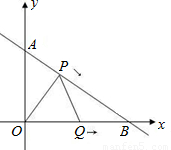
已知Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以O为坐标原点建立如图所示的直角坐标系,设P、Q分别为AB、OB边上的动点,他们同时分别从点A、O向B点匀速移动,移动的速度都是1厘米/秒,设P、Q移动时间为 t秒(0≤t≤4)
t秒(0≤t≤4)(1)试用t的代数式表示P点的坐标;
(2)求△OPQ的面积S(cm2)与t(秒)的函数关系式;当t为何值时,S有最大值,并求出S的最大值;
(3)试问是否存在这样的时刻t,使△OPQ为直角三角形?如果存在,求出t的值,如果不存在,请说明理由.
分析:(1)作PM⊥OA于M,则PM∥OB,再根据平行线分线段成比例定理列出比例式;由勾股定理求出AB=5,而AP=t,根据比例式求出AM、PM的值,P点坐标即可得到;
(2)根据三角形的面积公式,P点纵坐标与OQ的长度的积的一半就是△OPQ面积,整理后根据二次函数的最值问题求解即可;
(3)作OQ边上的高,根据△PON和△QPN相似,相似三角形对应边成比例,列式求解.
(2)根据三角形的面积公式,P点纵坐标与OQ的长度的积的一半就是△OPQ面积,整理后根据二次函数的最值问题求解即可;
(3)作OQ边上的高,根据△PON和△QPN相似,相似三角形对应边成比例,列式求解.
解答: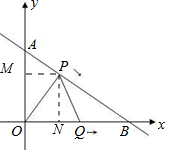 解:(1)作PM⊥OA于M,则PM∥OB,
解:(1)作PM⊥OA于M,则PM∥OB,
∴AM:AO=PM:BO=AP:AB,
∵OA=3cm,OB=4cm,
∴在Rt△OAB中,AB=
=
=5cm,
∵AP=1•t=t,
∴
=
=
,
∴PM=
t,AM=
t,
∴OM=OA-AM=3-
t,
∴点P的坐标为(
t,3-
t);
(2)∵OQ=1•t=tcm,
∴S△OPQ=
×t×(3-
t)=-
t2+
t=-
(t-
)2+
,
∴当t=
s时,S有最大值,最大值为
cm2;
(3)存在.
理由:作PN⊥OB于N,
∵△OPQ为直角三角形,
∴△PON∽△QPN,
∴
=
,
∴(3-
t)2=
t(t-
t),
解得t1=3,t2=15(舍去);
∴当t=3s时,△OPQ为直角三角形.
 解:(1)作PM⊥OA于M,则PM∥OB,
解:(1)作PM⊥OA于M,则PM∥OB,∴AM:AO=PM:BO=AP:AB,
∵OA=3cm,OB=4cm,
∴在Rt△OAB中,AB=
| OA2+OB2 |
| 32+42 |
∵AP=1•t=t,
∴
| AM |
| 3 |
| PM |
| 4 |
| t |
| 5 |
∴PM=
| 4 |
| 5 |
| 3 |
| 5 |
∴OM=OA-AM=3-
| 3 |
| 5 |
∴点P的坐标为(
| 4 |
| 5 |
| 3 |
| 5 |
(2)∵OQ=1•t=tcm,
∴S△OPQ=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 3 |
| 2 |
| 3 |
| 10 |
| 5 |
| 2 |
| 15 |
| 8 |
∴当t=
| 5 |
| 2 |
| 15 |
| 8 |
(3)存在.
理由:作PN⊥OB于N,
∵△OPQ为直角三角形,
∴△PON∽△QPN,
∴
| PN |
| QN |
| ON |
| PN |
∴(3-
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
解得t1=3,t2=15(舍去);
∴当t=3s时,△OPQ为直角三角形.
点评:此题考查了勾股定理,平行线分线段成比例定理,二次函数最值问题以及相似三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是数形结合思想与函数思想的应用,注意辅助线的作法.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒. 如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求:
如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求: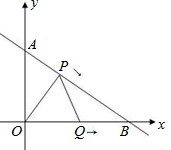 t秒(0≤t≤4)
t秒(0≤t≤4)