摘要：数形结合题 例3 如图1,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分剪拼成一个矩形,通过计算两个图形阴影部分的面积,验证了一个等式,则这个等式是( ) A.a2-b2=2=a2+2ab+b2 C.(a-b)2=a2-2ab+b2 D.=a2+ab-2b2 解:由题意得阴影部分的面积相等,图(1)的面积为a2-b2;图(2)中,宽为a-b,长为a+b,面积为,所以有a2-b2=,故选A. 点评:此题解题的关键是找到等量关系和变化后边长的变化. 中考数学基础达标验收卷
网址：http://m.1010jiajiao.com/timu3_id_456291[举报]
如图1，正方形ABCD，△AMN是等腰Rt△，∠AMN=90°，当Rt△AMN绕点A旋转时，边AM、AN分别与BC（或延长线图3）、CD（或延长线图3）相交于点E、F，连接EF，小明与小红在研究图1时，发现有这么一个结论：EF=DF+BE；为了解决这个问题，小明与小红，经过讨论，采取了以下方案：延长CB到G，使BG=DF，连接AG，得到图2，请你根据小明、小红的思路，结合图2，解决下列问题：
（1）证明：①△ADF≌△ABG； ②EF=DF+BE；
（2）根据图（3），①结论EF=DF+BE是否成立，如不成立，写出三线段EF、DF、BE的数量关系并证明．②若CE=6，DF=2，求正方形ABCD的边长．
查看习题详情和答案>>
（1）证明：①△ADF≌△ABG； ②EF=DF+BE；
（2）根据图（3），①结论EF=DF+BE是否成立，如不成立，写出三线段EF、DF、BE的数量关系并证明．②若CE=6，DF=2，求正方形ABCD的边长．
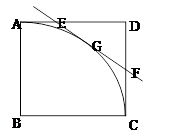
如图，在正方形ABCD中，AB＝1，AC是以点B为圆心，AB长为半径的圆的一条弧，点E是边AD上的任意一点（点E与A、D不重合），过E作AC所在圆的切线，交边DC于点F，G为切点
【小题1】当∠DEF＝
时，试说明点G为线段EF的中点；
【小题2】设AE＝
，FC＝
，用含有的代数式来表示，并写出的取值范围
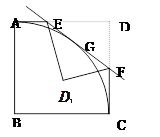
【小题3】如果把△DEF沿直线EF对折后得△
，如图2，当
时，讨论△
与△
是否相似，如果相似，请加以证明；如果不相似，只要写出结论，不要求写出理由．
查看习题详情和答案>>
【小题1】当∠DEF＝
时，试说明点G为线段EF的中点；【小题2】设AE＝
，FC＝，用含有的代数式来表示，并写出的取值范围【小题3】如果把△DEF沿直线EF对折后得△
，如图2，当 时，讨论△与△是否相似，如果相似，请加以证明；如果不相似，只要写出结论，不要求写出理由．
查看习题详情和答案>>
如图，已知正方形ABCD，点P为射线BA上的一点（不和点A，B重合），过P作PE⊥CP，且CP＝PE．过E作EF∥CD交射线BD于F．
【小题1】若CB＝6，PB＝2，则EF＝ ；DF＝ ；
【小题2】请探究BF，DG和CD这三条线段之间的数量关系，写出你的结论并证明；
【小题3】如图2，点P在线段BA的延长线上，当tan∠BPC＝ 时，四边形EFCD与四边形PEFC的面积之比为
．
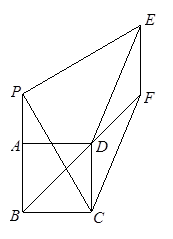查看习题详情和答案>>
【小题1】若CB＝6，PB＝2，则EF＝ ；DF＝ ；
【小题2】请探究BF，DG和CD这三条线段之间的数量关系，写出你的结论并证明；
【小题3】如图2，点P在线段BA的延长线上，当tan∠BPC＝ 时，四边形EFCD与四边形PEFC的面积之比为
．
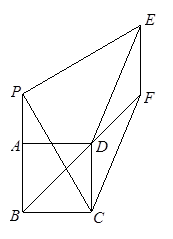查看习题详情和答案>>
．
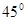时，试说明点G为线段EF的中点；
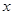，FC＝
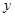，用含有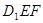
，如图2，当
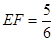时，讨论△
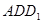与△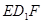
是否相似，如果相似，请加以证明；如果不相似，只要写出结论，不要求写出理由．
