题目内容
如图,已知正方形ABCD,点P为射线BA上的一点(不和点A,B重合),过P作PE⊥CP,且CP=PE.过E作EF∥CD交射线BD于F.
【小题1】若CB=6,PB=2,则EF= ;DF= ;
【小题2】请探究BF,DG和CD这三条线段之间的数量关系,写出你的结论并证明;
【小题3】如图2,点P在线段BA的延长线上,当tan∠BPC= 时,四边形EFCD与四边形PEFC的面积之比为 .
.
【小题1】EF=6;DF=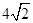
【小题2】BF+2DG= CD.
CD.
理由如下:如图⑴,连接AE,AC. 
∵△EPC为等腰Rt△;四边形ABCD为正方形,
∴
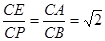 .
.
∠ECP=∠ACB=45°,
∴∠ECA=∠PCB.
∴△EAC∽△PCB. ………………………4分
∴∠EAC=∠PBC=90°.
∵∠BAC=∠ABD=45°,
∴∠EAB+∠ABF=180°.
∴EA∥BF.
又AB∥EF,
∴四边形EABF为平行四边形.………………5分
∴EF=AB=CD.
又∵AB∥CD,
∴EF∥CD.
∴△EFG∽△CDG .
∴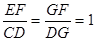 .………………………………………………………6分
.………………………………………………………6分
∴DF=2GF=2DG.……………………………………………………7分
∴BF+2DG=BD= CD.……………………………………………8分
CD.……………………………………………8分
【小题3】tan∠BPC=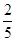 或
或 .…………………………………………………10分
.…………………………………………………10分
解析

练习册系列答案
相关题目
 如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM.
如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM. (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( )
如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( ) 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.