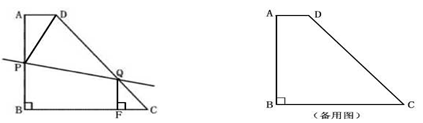
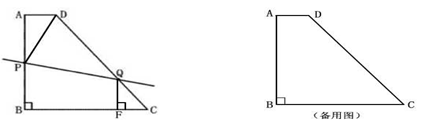
摘要：)如图.已知直角梯形ABCD中.AD∥BC.ÐB＝90º.AB＝12cm.BC＝8cm,DC＝13cm.动点P沿A→D→C线路以2cm/秒的速度向C运动.动点Q沿B→C线路以1cm/秒的速度向C运动.P.Q两点分别从A.B同时出发.当其中一点到达C点时.另一点也随之停止.设运动时间为t秒.△PQB的面积为ym2. (1)求AD的长及t的取值范围, (2)当1.5≤t≤t0(t0为时.求y关于t的函数关系式, (3)请具体描述:在动点P.Q的运动过程中.△PQB的面积随着t的变化而变化的规律.
网址：http://m.1010jiajiao.com/timu3_id_455461[举报]
如图，已知直角梯形ABCD中，AD∥BC，∠DAB=90°，且AD=DC；以A为圆心，AB为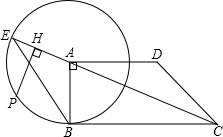
半径作⊙A，交CA延长线于点E．
（1）求证：直线DC是⊙A的切线；
（2）若P是
的中点，作PH⊥AE于H，若PH=5，sin∠ABE=
，求AB的长．
查看习题详情和答案>>
半径作⊙A，交CA延长线于点E．（1）求证：直线DC是⊙A的切线；
（2）若P是
 |
| BE |
| 3 |
| 5 |
如图，已知直角梯形ABCD中，AD∥BC，∠BCD=90°，BC=CD=2AD，E、F分别是BC、CD边的中点，连接BF、DE交于点P，连接CP并延长交AB于点Q，连接AF，则下列结论：①CP平分∠BCD；②四边形ABED为平行四边形；③CQ将直角梯形ABCD分为面积相等的两部分；④△ABF为等腰三角形，其中不正确的有（ ）
查看习题详情和答案>>
如图，已知直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C=60°，以AB为一边作等边三角形ABE，点E正好落在CD上．（1）填空：∠BEC=
90
90
度；（2）试说明：BC=DC．
