Question

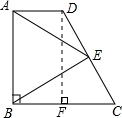
如图，已知直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C=60°，以AB为一边作等边三角形ABE，点E正好落在CD上．
（1）填空：∠BEC=

90

度；
（2）试说明：BC=DC．

Answer 1

分析：（1）根据等边三角形的性质得到∠ABE=60°，由∠ABC=90°即可求出∠EBC=30°，由已知的∠C的度数，根据三角形的内角和定理即可求出∠BEC的度数；
（2）作DF⊥BC，垂足为点F，即可得到四边形ABFD为矩形，根据矩形的性质得到AB=DF，又由等边三角形的性质得到AB=BE，等量代换得到BE=DF，再加一对直角和一对公共角的相等，根据“AAS”得到△BEC≌△DFC，最后根据全等三角形的对应边相等即可得证．

解答：解：（1）∵△ABE为等边三角形，
∴∠ABE=60°，
又∠ABC=90°，
∴∠EBC=90°-60°=30°，
∵∠C=60°，
∴∠BEC=180°-∠C-∠EBC=90°；（2分）
（2）作DF⊥BC，垂足为点F，则四边形ABFD为矩形，

∵四边形ABFD为矩形，
∴AB=DF，
∵△ABE为等边三角形，
∴AB=BE，
∴BE=DF，
在△BEC与△DFC中，

∠BEC=∠DFC=90° ∠C=∠C BE=DF

，
∴△BEC≌△DFC（AAS），
∴BC=DC．
故答案为：90．

点评：此题考查了等边三角形的性质，矩形的性质以及全等三角形的性质与判定，全等三角形的判定方法有：SSS，ASA，AAS，SAS，HL（直角三角形），要求学生根据题意灵活选择合适的方法，利用三角形的全等可解决边或角相等的问题．