摘要：19．如图.在梯形ABCD中.AD∥BC.M.N分别是AB.CD的中点.ME∥AN交BC于点E.求证AM＝NE． [提示]延长AN交BC延长线于点F．证明NE为△ABF的中位线． [答案]延长AN交BC的延长线于点F. ∵ DN＝CN.∠AND＝FNC. 又由AD∥BC.得∠ADN＝∠FCN. ∴ △ADN≌△FCN． ∴ AN＝NF． ∵ AM＝BM且ME∥AF. ∴ BE＝EF． ∴ NE为△ABF的中位线. ∴ NE＝AB＝AM．
网址：http://m.1010jiajiao.com/timu3_id_455181[举报]
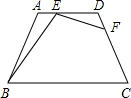如图，在梯形ABCD中，AD∥BC，AB=DC=AD=6，点E、F分别在线段AD、DC上（点E与点A、D不重合），若∠ABC=60°，∠BEF=120°，AE=x，DF=y，则y关于x的函数关系式为
如图，在梯形ABCD中，AD∥BC，若E，F，G，H分别是梯形ABCD各边AB、BC、CD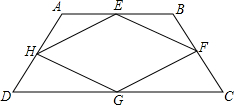
、DA的中点．
（1）求证：四边形EFGH平行四边形；
（2）当梯形ABCD满足什么条件时，四边形EFGH是菱形；
（3）在（2）的条件下，梯形ABCD满足什么条件时，四边形EFGH是正方形． 查看习题详情和答案>>
、DA的中点．（1）求证：四边形EFGH平行四边形；
（2）当梯形ABCD满足什么条件时，四边形EFGH是菱形；
（3）在（2）的条件下，梯形ABCD满足什么条件时，四边形EFGH是正方形． 查看习题详情和答案>>
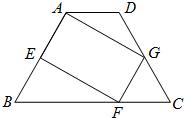24、如图，在梯形ABCD中，AD∥BC，AB=DC．点E、F、G分别在边AB、BC、CD上，AE=GF=GC．（1）求证：四边形AEFG是平行四边形；
（2）当∠FGC=2∠EFB时，求证：四边形AEFG是矩形．
如图，在梯形ABCD中，AD∥BC，M，N分别是AD，BC的中点，若∠B与∠C互余，则MN与BC-AD的关系是（ ）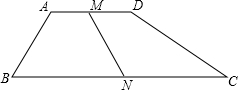
| A、2MN＜BC-AD | B、2MN＞BC-AD | C、2MN=BC-AD | D、MN=2（BC-AD） |
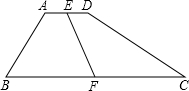如图，在梯形ABCD中，AD∥BC，∠B+∠C=90°，AD=1，BC=3，E、F分别是AD、BC的中点，则EF=