摘要:如图. 等腰梯形ABCD中.AB=15.AD=20.∠C=30º.点M.N同时以相同速度分别从点A.点D开始在AB.AD设ND的长为x.用x表示出点N到AB的距离.并写出x的取值范围. (2)当五边形BCDNM面积最小时.请判断△AMN的形状. 解:(1)过点N作BA的垂线NP.交BA的延长线于点P. ------ 由已知.AM=x.AN=20-x. ∵ 四边形ABCD是等腰梯形.AB∥CD.∠D=∠C=30º. ∴ ∠PAN=∠D=30º. 在Rt△APN中.PN=ANsin∠PAN=(20-x). 即点N到AB的距离为(20-x). ------------ ∵ 点N在AD上.0≤x≤20.点M在AB上.0≤x≤15. ∴ x的取值范围是 0≤x≤15. ------------.S△AMN=AM•NP=x(20-x)=. -- ∵ <0.∴ 当x=10时.S△AMN有最大值. ---------- 又∵ S五边形BCDNM=S梯形-S△AMN.且S梯形为定值. ∴ 当x=10时.S五边形BCDNM有最小值. ---------- 当x=10时.即ND=AM=10.AN=AD-ND=10.即AM=AN. 则当五边形BCDNM面积最小时.△AMN为等腰三角形. ----
网址:http://m.1010jiajiao.com/timu3_id_455118[举报]
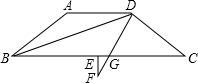 如图,等腰梯形ABCD,AD∥BC,AB=CD,BD平分∠ABC,点E为BC中点,EF⊥BC,DF=DC,DF交BC于点G,若EG=1,BE=9,则AD=
如图,等腰梯形ABCD,AD∥BC,AB=CD,BD平分∠ABC,点E为BC中点,EF⊥BC,DF=DC,DF交BC于点G,若EG=1,BE=9,则AD=
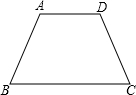 如图,等腰梯形ABCD中,AD∥BC,AB=CD.且∠B=60°,AD=AB=4.
如图,等腰梯形ABCD中,AD∥BC,AB=CD.且∠B=60°,AD=AB=4. 4、如图,等腰梯形ABCD中,AD∥BC,若将腰AB沿A?D的方向平移到DE的位置,则图中与∠C相等的角(不包括∠C)有( )
4、如图,等腰梯形ABCD中,AD∥BC,若将腰AB沿A?D的方向平移到DE的位置,则图中与∠C相等的角(不包括∠C)有( )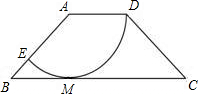 如图,等腰梯形ABCD中,AD∥BC,以A为圆心,AD为半径的圆与BC相切于点M,与AB相交于点E,若AD=2,BC=6,则扇形DAE的面积为( )
如图,等腰梯形ABCD中,AD∥BC,以A为圆心,AD为半径的圆与BC相切于点M,与AB相交于点E,若AD=2,BC=6,则扇形DAE的面积为( )