题目内容
如图,等腰梯形ABCD的顶点都在小正方形的顶点上,能否在DC上找到一点E使得梯形被EA、EB分割成3个相似三角形?如果能,请用符号把它们表示出来,并求相似比;若不能,请说明理由.
分析:由图形可知∠A=∠B=45°,∠D=∠C=135°,AD和BC的长也可求,若要使△ADE∽△ECB.则可选择尝试SAS判定法,取E 在D右边一格顶点上即DE=
CE问题即可解决.再通过勾股定理计算AE,BE的值利用SAS判定△BEA∽△ADE,所以三个三角形都相似.
| 1 |
| 2 |
解答:解:能在DC上找到一点E使得梯形被EA、EB分割成3个相似三角形,点E 在D右边一格顶点上即DE=
CE(如图所示)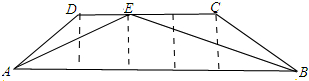
连接AE,BE,
设每个小正方形的边长为1,
∴AD=BC=
=
.
∵
=
,
=
=
,
又∵等腰梯形ABCD的顶点都在小正方形的顶点上,
∴∠DAB=∠CBA=45°,
∴∠ADE=135°,∠ECB=135°.
∴△ADE∽△ECB.
∴∠AED=∠CBE.
∵∠CEB+∠CBE=45°,
∴∠AED+∠CEB=45°,
∴∠AEB=135°,
由图知AE=
=
,EB=
=
.
∴
=
=
,
∴△BEA∽△ADE∽△ECB.
∴能在DC上找到一点E使得梯形被EA、EB分割成3个相似三角形.
它们的相似比为:ED:BC:AE=1:
:
.
| 1 |
| 2 |

连接AE,BE,
设每个小正方形的边长为1,
∴AD=BC=
| 12+12 |
| 2 |
∵
| AD |
| DE |
| ||
| 1 |
| CE |
| CB |
| 2 | ||
|
| ||
| 1 |
又∵等腰梯形ABCD的顶点都在小正方形的顶点上,
∴∠DAB=∠CBA=45°,
∴∠ADE=135°,∠ECB=135°.
∴△ADE∽△ECB.
∴∠AED=∠CBE.
∵∠CEB+∠CBE=45°,
∴∠AED+∠CEB=45°,
∴∠AEB=135°,
由图知AE=
| 12+22 |
| 5 |
| 12+32 |
| 10 |
∴
| BE |
| AE |
| ||
|
| ||
| 1 |
∴△BEA∽△ADE∽△ECB.
∴能在DC上找到一点E使得梯形被EA、EB分割成3个相似三角形.
它们的相似比为:ED:BC:AE=1:
| 2 |
| 5 |
点评:本题考查了相似三角形的判定和性质,常用的相似判定方法有:平行线,AA,SAS,SSS;常用到的性质:对应角相等;对应边的比值相等;面积比等于相似比的平方.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( ) 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.