摘要：四边形ABCD.DEFG都是正方形.连接AE.CG． (1)求证:AE=CG, (2)观察图形.猜想AE与CG之间的位置关系. 并证明你的猜想． (1) 证明: 如图. ∵ AD=CD.DE=DG.∠ADC=∠GDE=90o. 又 ∠CDG=90o +∠ADG=∠ADE. ∴ △ADE≌△CDG． ∴ AE=CG． (2)猜想: AE⊥CG． 证明: 如图. 设AE与CG交点为M.AD与CG交点为N． ∵ △ADE≌△CDG. ∴ ∠DAE=∠DCG． 又∵ ∠ANM=∠CND. ∴ △AMN∽△CDN． ∴ ∠AMN=∠ADC=90o．∴ AE⊥CG．
网址：http://m.1010jiajiao.com/timu3_id_455114[举报]
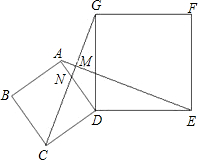如图，四边形ABCD、DEFG都是正方形，连接AE、CG，AE与CG相交于点M，CG与AD相交于点N．
22、如图，四边形ABCD、DEFG都是正方形，连接AE、CG，AE与CG相交于点M，CG与AD相交于点N．试判断AE与CG之间的关系？并说明理由．
如图，四边形ABCD和DEFG是两个边长相等的正方形，连接CE，若∠ADG=150°，则∠DCE=
（2013•历城区一模）如图，四边形ABCD、DEFG都是正方形，连接AE、CG，AE与CG相交于点M．下列结论：①AE=CG，②AE⊥CG，③DM∥GE，④OM=OD，⑤∠DME=45°．正确结论的个数为（ ）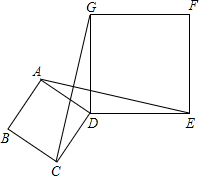
如图，四边形ABCD、DEFG都是正方形，连接AE、CG．观察图形，猜想AE与CG之间的位置关系，并证明你的猜想．