17、如图，在梯形纸片ABCD中，AB∥CD，AD=BC，AB=6，CD=3．将该梯形纸片沿对角线AC折叠，点D恰与AB边上的点E重合，则∠BCE=度．

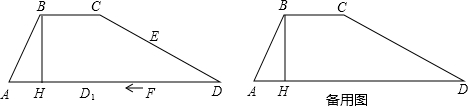
如图，在梯形纸片ABCD中，BC∥AD，∠A+∠D=90°，tanA=2，过点B作BH⊥AD于H，BC=BH=2．动点F从点D出发，以每秒1个单位的速度沿DH运动到点H停止，在运动过程中，过点F作FE⊥AD交折线D-C-B于点E，将纸片沿直线EF折叠，点C、D的对应点分别是点C₁、D₁．设F点运动的时间是x秒（x＞0）．
（1）当点E和点C重合时，求运动时间x的值；
（2）在整个运动过程中，设△EFD₁或四边形EFD₁C₁与梯形ABCD重叠部分面积为S，请直接写出S与x之间的函数关系式和相应自变量x的取值范围；
（3）平移线段CD，交线段BH于点G，交线段AD于点P．在直线BC上存在点I，使△PGI为等腰直角三角形．请求出线段IB的所有可能的长度．

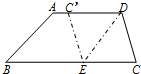21、如图，在梯形纸片ABCD中，AD∥BC，AD＞CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C’处，折痕DE交BC于点E，连接C’E，试判断四边形CDC’E是什么特殊四边形，并说明理由．

23、如图，在梯形纸片ABCD中，AD∥BC，AD＞CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连接C′E．
求证：四边形CDC′E是菱形．

19、如图，在梯形纸片ABCD中，AD∥BC，AD＞CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C′处，折痕DE交BC于点E，连接C′E．
（1）求证：四边形CDC′E是菱形；
（2）若BC=CD+AD，试判断四边形ABED的形状，并加以证明．